P13-Ejercico 3

P13-Ejercico 3

de Diego Ismael Marichal Chavez -
Número de respuestas: 5

Hola, no estoy entendiendo si lo que me pide es la amplitud de las oscilaciones o otra amplitud, tenia entendido que la amplitud de oscilaciones la denotamos con la A, en la ecuación de movimiento. Pero resolviendo el ejercicio no se como vincular la ecuación de movimiento, viendo vídeos de docentes donde se resuelve el ejercicio, pareciera que toman la amplitud máxima como la distancia desde la posición natural del resorte, pero no entiendo porque seria la amplitud, no seria el estiramiento máximo para que no deslicen las masas?

Utilizan esta realacion: |a|= A w^2

Pero en el teorico lo vimos como: a = -x w^2

Porque x seria la amplitud?

Saludos

Diego



En respuesta a Diego Ismael Marichal Chavez

Re: P13-Ejercico 3

de Florencia Benitez Martinez -
Hola Diego.
En un oscilador, la posición en función del tiempo está dada por x(t)=A cos(wt), donde A es la amplitud de la posición.
Lo que pide es el máximo valor que puede tener esa amplitud de manera que los bloques no deslicen.
Eso depende de la aceleración, por eso se utilizan la relación: a_max= A w^2. Este es el valor máximo que toma la aceleración en un oscilador. La expresión que mencionás: a = -x w^2, es la función a(t).
Si se deriva dos veces x(t), se obtiene: a(t)= - w^2 x(t) = - w^2 A cos(wt) (de ahí viene la relación a_max= A w^2).
Saludos!
En respuesta a Florencia Benitez Martinez

Re: P13-Ejercico 3

de Agustín Arístides Almeida Ahlers -
Buenas, hay algo que no comprendo. Si la aceleración es máxima entonces el sistema está en la posición máxima que interpreto es A en la ecuación de posición en función del tiempo. Pero cuando quiero despejar A me encuentro con la frecuencia angular al cuadro y no entiendo cómo podría hallarlo. Me encuentro en esta situación:
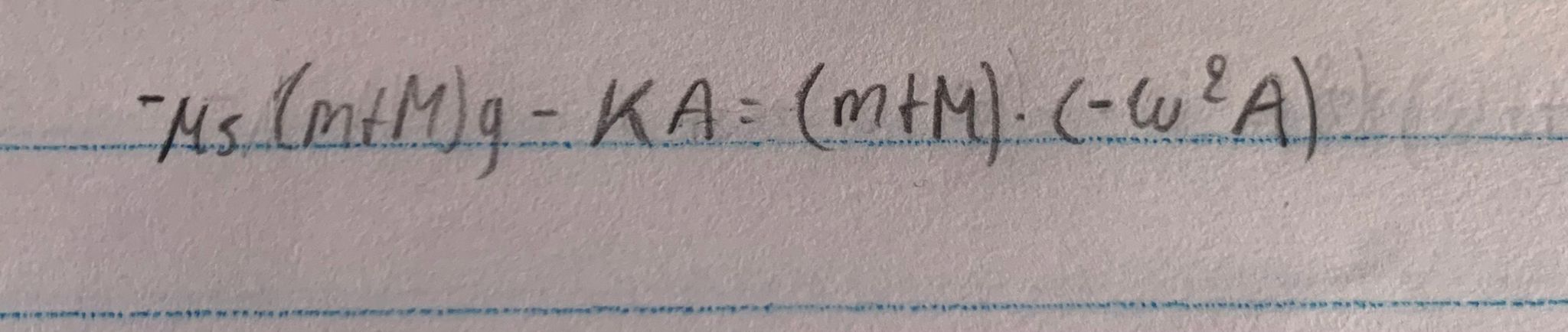
Adjunto amplitud.jpeg
En respuesta a Agustín Arístides Almeida Ahlers

Re: P13-Ejercico 3

de Florencia Benitez Martinez -
Hola Agustín,
¿cómo se relaciona la frecuencia angular con los parámetros del problema? Quizá puedas recordarlo escribiendo la ecuación de movimiento para un sistema masa (m) - resorte (k).
Intentalo y, en todo caso, volvé a consultar.
Saludos!
En respuesta a Florencia Benitez Martinez

Re: P13-Ejercico 3

de Agustín Arístides Almeida Ahlers -
Para el sistema masa (m) - resorte (k) obtengo que w2 = \sqrt[2]{k/m} pero en este caso como el sistema se mueve como todo uno interpretaría que ahora es w2= \sqrt[2]{k/m+M} pero sin embargo también actúa la fuerza rozamiento aunque interpreto que como no multiplica a x entonces no afecta al valor de la frecuencia angular.
Ahora, cuando sustituyo en la ecuación que había obtenido me queda en ambos lados de la ecuación el término -KA ¿qué error estaría cometiendo?
Desde ya gracias.
En respuesta a Agustín Arístides Almeida Ahlers

Re: P13-Ejercico 3

de Florencia Benitez Martinez -
Hola Agustín,
fijate que te pide la amplitud máxima para que no deslicen. Ese deslizamiento está determinado por la aceleración máxima y, en un oscilador, esta toma su valor máximo en los extremos (cuando está más alejado de la posición de equilibrio). Esto significa que deberías considerar esa posición para resolver el problema.
Saludos!