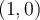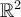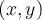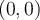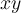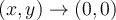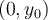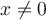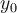Buenas me surgió una duda a la hora de estudiar la continuidad de la función de este ejercicio.
Quiero ver si f es cont. en los puntos de la forma 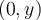 que es donde hay problemas. Mi intención es calcular
que es donde hay problemas. Mi intención es calcular  y ver si eso es igual a
y ver si eso es igual a  .
.
Se puede pensar como un limite de una sola variable dado que la y es "libre" o sea  ? Esto seria asi con la intencion de usar la equivalencia
? Esto seria asi con la intencion de usar la equivalencia  cuando
cuando 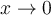
Saludos.