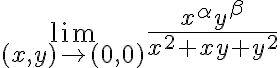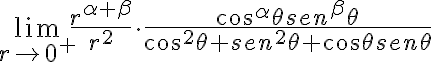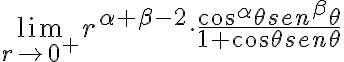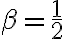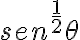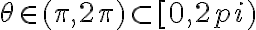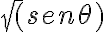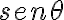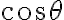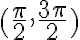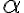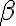Foro Práctico 7

Buenas, hay algo que no termino de entender de este ejercicio

Cuando nos piden calcular $\lim_{(x,y) \to (0,0)} \frac{x^{\alpha}y^{\beta}}{x^{2}+xy+y^{2}}$

Lo que hice, luego de unos intentos, fue pasar a coordenadas polares y estudiar 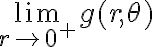$\lim_{r \to 0^{+}} g(r,\theta)$

Entonces quedo 

$\lim_{r \to 0^{+}} \frac{r^{\alpha + \beta}}{r^{2}} \cdot \frac{cos^{\alpha}\theta sen^{\beta}\theta}{cos^{2}\theta + sen^{2}\theta +cos\theta sen\theta}$

$\lim_{r \to 0^{+}} r^{\alpha + \beta - 2} \cdot \frac{cos^{\alpha}\theta sen^{\beta}\theta}{1 + cos\theta sen\theta}$

Luego empece por estudiar la acotación de la función que depende del angulo 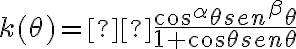$k(\theta) = \frac{cos^{\alpha}\theta sen^{\beta}\theta}{1 + cos\theta sen\theta}$

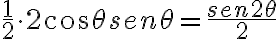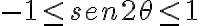Se cumple que $\frac{1}{2} \cdot 2 cos\theta sen\theta = \frac{sen2\theta}{2}$ Como  $-1 \leq sen2\theta \leq 1$ entonces 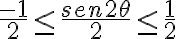$\frac{-1}{2} \leq \frac{sen2\theta}{2} \leq \frac{1}{2}$ Y por lo tanto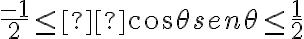 $\frac{-1}{2} \leq cos\theta sen\theta \leq \frac{1}{2}$

Finalmente 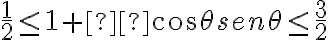$\frac{1}{2} \leq 1 + cos\theta sen\theta \leq \frac{3}{2}$ por lo que tenemos acotado el denominador de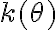 $k(\theta)$

 Para acotar 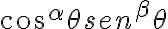$cos^{\alpha}\theta sen^{\beta}\theta$ es que me surgen algunas dudas.

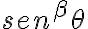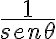Tomando como ejemplo $sen^{\beta}\theta$ es claro que si $\beta < 0$ entonces se obtiene algo de la forma $\frac{1}{sen\theta}$ que no es acotado.

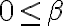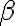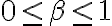La duda en si es si alcanza con pedir que $0 \leq \beta$ Que pasa con los $\beta$ que cumplen $0 \leq \beta \leq 1$ ?

Por ejemplo si $\beta = \frac{1}{2}$ que sucede con $sen^{\frac{1}{2}}\theta$ cuando $\theta \in (\pi, 2\pi) \subset [0,2pi)$ ?