Hola Pablo!
En estos ejercicios creo que lo imortante es entender qué forma tienen los conjuntos de nivel y que, hasta cierto nivel de detalle, uno sea capaz de escribirlos explícitamente. Esto lo digo porque, en cuanto a definición de conjunto, uno podría "resolver" todo el ejercicio 2 sin hacer ningún desarrollo, solo planteando la definición de conjunto de nivel y como definición de conjunto sería correcta. Sin embargo, resolverlo así no te aporta nada al momento de entender cómo puede ser el comportamiento de la función, o si se quisiese graficar después. Para esto está bueno poder escribir a los conjuntos de nivel como curvas conocidas (circunferencias, casarones esféricos, elipses) o funciones, dando más detalle acerca de como se componen. Que tengas alguna intuición gráfica de cómo se forma el conjunto que escribís en la solución.
Teniendo esto en mente, en la parte b algo que uno puede identificar es que las curvas de nivel se forman por "cascarones esféricos" (la superficie de una esfera) concéntricos en el origen. Es decir, la función se puede escribir simplemente como función de la norma del punto:
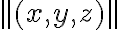
. Finalmente, se describe al conjunto de nivel como los
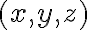
tales que su norma pertenezca a
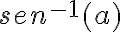
, el conjunto preimagen de
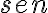
en

. Este conjunto es algo engorroso de describir, pero es un problema de cálculo 1. Quizás lo que está bueno es ser consciente de que entre

y
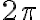
, en general hay 2 ángulos que tienen el mismo seno, y si luego a cada uno le sumo
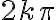
en ángulos puede encontrar el conjunto preimagen. Esto daría lugar a infinitos cascarones esféricos concéntricos en el origen que tienen la misma imágen.
Para la parte c, tenés que analizar según los casos de a. Para a distinto de 0, también se reduce a cascarones esféricos concéntricas, pero no en el origen. Te aconsejo que plantees la igualdad, pases multiplicando el denominador, e intentes de encontrar una expresión de la forma:
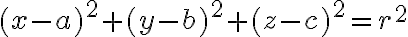
, dado que ahí sabés el centro y el radio del cascarón esférico en cuestión.
Avisame si te surgen más dudas después de probar con esto.
Saludos!
Rodrigo


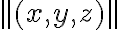 . Finalmente, se describe al conjunto de nivel como los
. Finalmente, se describe al conjunto de nivel como los 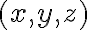 tales que su norma pertenezca a
tales que su norma pertenezca a 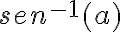 , el conjunto preimagen de
, el conjunto preimagen de 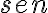 en
en  . Este conjunto es algo engorroso de describir, pero es un problema de cálculo 1. Quizás lo que está bueno es ser consciente de que entre
. Este conjunto es algo engorroso de describir, pero es un problema de cálculo 1. Quizás lo que está bueno es ser consciente de que entre  y
y 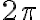 , en general hay 2 ángulos que tienen el mismo seno, y si luego a cada uno le sumo
, en general hay 2 ángulos que tienen el mismo seno, y si luego a cada uno le sumo 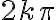 en ángulos puede encontrar el conjunto preimagen. Esto daría lugar a infinitos cascarones esféricos concéntricos en el origen que tienen la misma imágen.
en ángulos puede encontrar el conjunto preimagen. Esto daría lugar a infinitos cascarones esféricos concéntricos en el origen que tienen la misma imágen.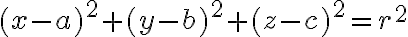 , dado que ahí sabés el centro y el radio del cascarón esférico en cuestión.
, dado que ahí sabés el centro y el radio del cascarón esférico en cuestión.