Hola, voy respondiendo por partes:
-- Sobre

, es como dice Julieta. Da

porque los extremos quedan al revés:

.
-- Sobre la continuidad de
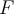
, es verdad que es una función continua. No me doy cuanta por qué el hecho de que

sea

te hace pensar que no queda continua en 1. (En el siguiente punto va a queda más claro cómo es
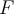
.)
-- Sobre la duda de Gabriel. En este caso, la función
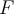
no va a tener una sola formulita como la que planteás. Vamos a resolverlo explícitamente, separando en casos.
Primer caso, me agarro un
![x\in[1,3] x\in[1,3]](https://eva.fing.edu.uy/filter/tex/pix.php/3922e65987a09850f900fb4863269f95.png)
. Si pintamos la región correspondiente al área

, vemos que esta es la unión de un rectángulo de área
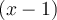
con un triángulo de área

. La suma de estas dos áreas da

. Así que sí, es como decís vos; para
![x\in[1,3] x\in[1,3]](https://eva.fing.edu.uy/filter/tex/pix.php/3922e65987a09850f900fb4863269f95.png)
tenemos

.
El problema es que la fórmula anterior no vale para los números menores que 1. En particular, no vale usarla para calcular

. Así que nada, entramos al segundo caso, en donde nos agarramos un

. Lo primero que arreglamos es el tema de que los extremos "quedan al revés". Simplemente escribimos

, para

. Ahora, si pintamos la región correspondiente al área

, vemos que esta es un rectángulo de área

. Entonces obtenemos

para

.
Conclusión, la
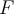
queda definida partida con dos formulitas, dependiendo de si

o
![x\in[1,3] x\in[1,3]](https://eva.fing.edu.uy/filter/tex/pix.php/3922e65987a09850f900fb4863269f95.png)
. La formulita para el primer intervalo es

, y la segunda es

. (Notar que esta función es creciente y continua en todo punto.)



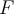
![x\in[1,3] x\in[1,3]](https://eva.fing.edu.uy/filter/tex/pix.php/3922e65987a09850f900fb4863269f95.png)