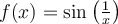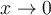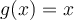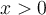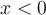Hola, vi la solución, pero no me quedó clara la resolución del ejercicio 3 de múltiple opción.
Entiendo que el límite de g(x) cuando x tiende a 0 sea justamente, 0. Y asumo que el límite de f(x) en 0 no existe porque (1/x) tiende a infinito, donde la función seno oscila. Pero si el límite de f(x) en 0 no existe, ¿por qué se sí existe el límite del producto con g(x) y no el de la suma con g(x)?
Multiplicar 0 por lo que sea da 0, pero incluso si ese algo no existe?