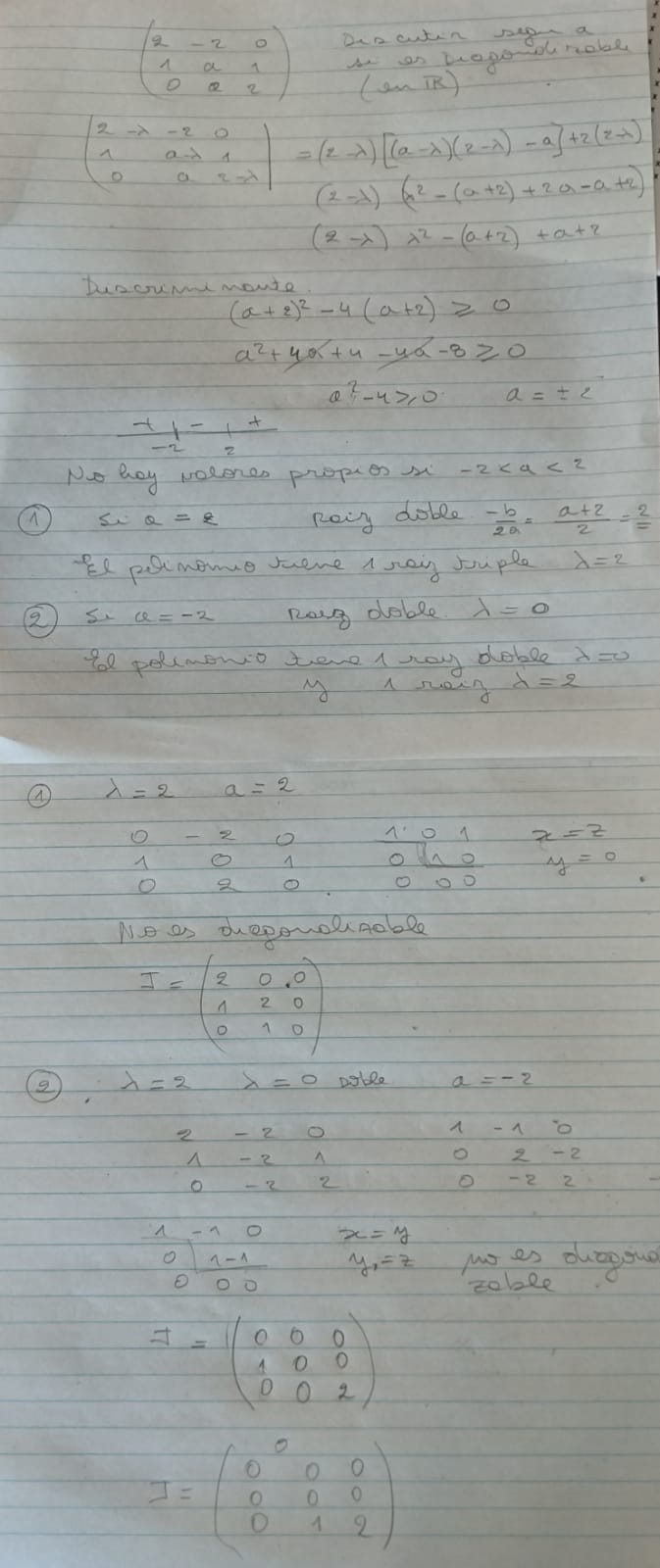Si el poliniomio caracteristico no tiene raices reales. Se halla la forma de jordan???
Encontre dos valores de a para los que me da raiz doble distinta de 2 pero no me doy cuenta por que no me dan los vectores propios para saber si es diagonalizable con ellos
otra cosa no será que en la matriz que nos da abajo es -a ( en la última fila) o 2 en la columna del medio???