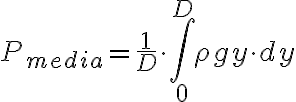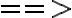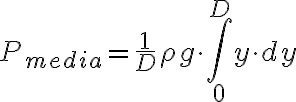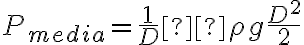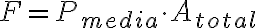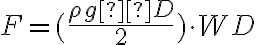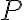Foro de Consultas Ejercicios y Teórico

Buenas, en una clase de practico hicimos este ejercicio de una forma distinta a como yo la hice y quería consultar si mi razonamiento es correcto.

En vez de escribir a la fuerza como 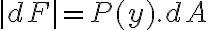$|dF| = P(y).dA$ e integrar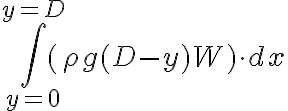 $\int_{y=0}^{y=D}(\rho g (D-y) W) \cdot dx$

Lo que hice fue hallar la presión media utilizando la definición de valor medio de una funcion (Calculus de Tom Apostol - pagina 145) y una vez que se tiene la presión media se la multiplica por el área total 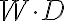$W \cdot D$. Queda entonces:

$P_{media} = \frac{1}{D}\cdot \int_{0}^{D} \rho g y \cdot dy$    $==>$    $P_{media} = \frac{1}{D} \rho g\cdot \int_{0}^{D} y \cdot dy$

$P_{media} = \frac{1}{D} \rho g \frac{D^{2}}{2}$    $==>$    $P_{media} = \frac{\rho g  D}{2}$  

Que al multiplicar por 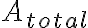$A_{total}$ se tiene:

$F = P_{media}\cdot A_{total}$   $==>$    $F = (\frac{\rho g  D}{2}) \cdot WD$

Que es la solución.

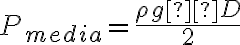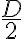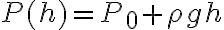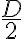Como bonus me gustaría preguntar si la presión media  $P_{media} = \frac{\rho g  D}{2}$  implica que la presión se aplica a $\frac{D}{2}$. Creo que esto no tiene sentido ya que la presión es una magnitud escalar. Pero es curioso que tenga la forma de la presión que varia según la altura, la expresión que es $P(h) = P_{0} +\rho g h$ en donde $h$ en este caso es $\frac{D}{2}$. Eso es por ser el valor medio?

Bueno, un saludos.

Nicolas