hola otra vez, disculpen también tengo problema con este :I en la parte a)
Aquí comienzo viendo que hay energía del peso y de los resortes, me guío por este dibujo que hice:
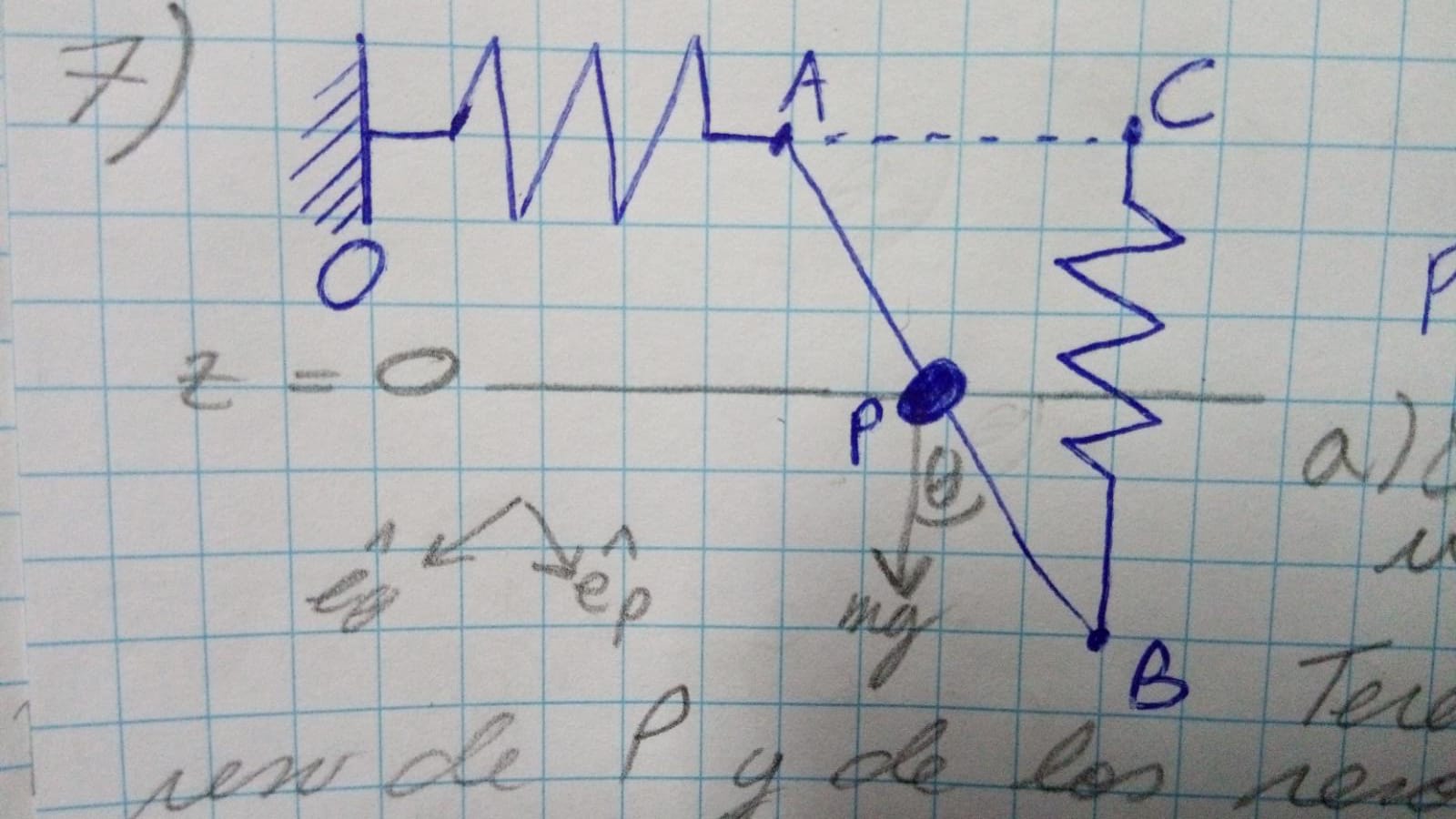
Si no mal tengo, para ver la energía es conveniente tomar una altura z=0, así que la tomo allí. Ésto me da estas relaciones:
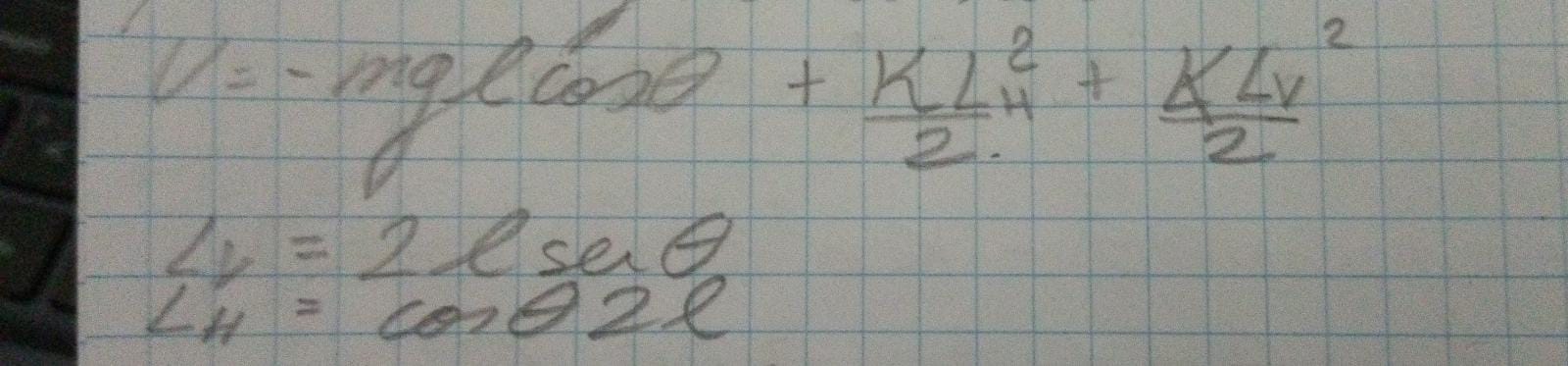
Luego la velocidad me da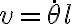 
pues l es constante. Luego como N⊥v=0 me parece, dE/dt =0 para la derivación más adelante, solo hay que derivar U + T = E pero el tema es que no me da correcto, hice ésto (usé la propiedad 
):
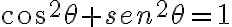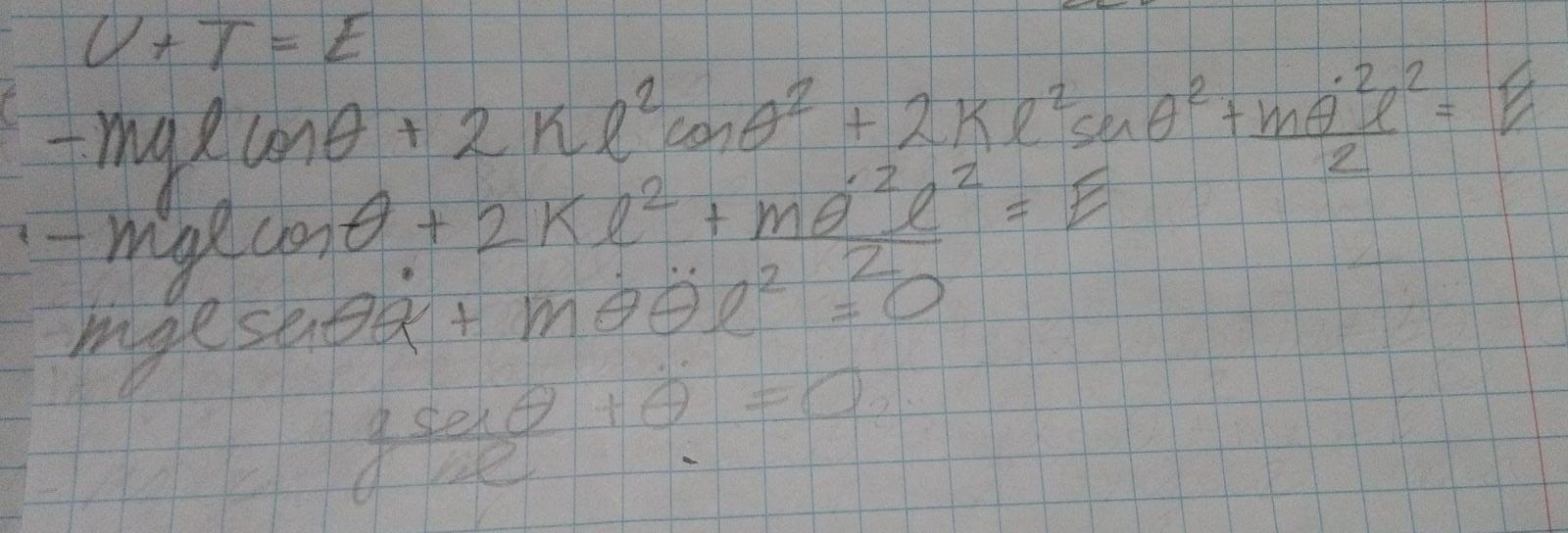
parece ser que me falta un término en coseno pero ni idea de dónde sale, probablemente sea de los resortes porque las cuentas no me dan la oportunidad de usar la sugerencia k=mg/4l, cuando derivé por tiempo sólo asumí que el ángulo cambiaba en el tiempo y por eso lo derivé así
gracias :)