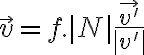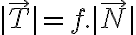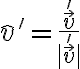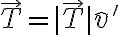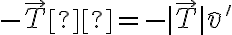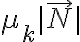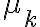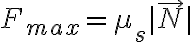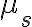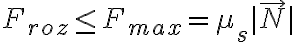Ejercicio 14 parte d)

Ejercicio 14 parte d)

de Nicolas Alejandro Scolaro Ribero -
Número de respuestas: 5

Buenas, tengo una duda con esta parte del ejercicio. Al intentar realizarla quise utilizar la expresión de fuerza de rozamiento dinámica (para un movimiento relativo) que es la siguiente:  \vec{v} = f. |N| \frac{ \vec{v'} }{|v'|}

En la solución de la letra no utiliza dicha expresión sino que pareciera que trabajara directamente con el módulo de la misma:  | \vec{T} | = f. | \vec{N} |

Claramente se trata más de una duda conceptual, a qué se debe esto? Es debido a que el vínculo es unilateral y no bilateral? Desde ya, muchas gracias. Saludos
En respuesta a Nicolas Alejandro Scolaro Ribero

Re: Ejercicio 14 parte d)

de Nicolás Casaballe -
Hola, Nicolás. Tu pregunta es bastante interesante.

Me da la impresión de que tu ecuación aparece una v en lugar de una T. ¿Puede ser?

Observa que lo que aparece en esa expresión vectorial es una técnica que "fabrica" un vector unitario con la misma dirección y sentido que la velocidad relativa:
\hat v' = \dfrac {\vec v'}{|\vec v'|}
 
Ya que la fuerza de fricción tiene la misma dirección y sentido que la velocidad relativa (*), entonces el vector de la fuerza de fricción se obtiene al multiplicar por el módulo:
\vec T = |\vec T| \hat v'

(*) Aparece la velocidad relativa porque la fricción siempre va en dirección contraria al deslizamiento entre las superficies. Hay que recordar que sobre cada superficie aparece una fuerza de fricción ejercida por la otra superficie. Como son una pareja de acción y reacción, también vemos la aparición de la fuerza - \vec T  = - |\vec T| \hat v' sobre el otro cuerpo.

Nota: cualquier vector siempre es igual al producto de su módulo por un vector unitario con su misma dirección y sentido.

En algunas situaciones sucede que conviene trabajar con el vector completo, mientras que otras veces (como en el ejercicio 14) se puede utilizar el módulo del vector. Una última observación para recordar: el módulo de cualquier vector siempre es positivo o cero; nunca negativo. 

Por esa razón, operar con módulos puede resultar engorroso, especialmente si tenemos la expectativa de que los vectores cambien de sentido cuando analizamos una situación física.

Saludos,
NC
En respuesta a Nicolás Casaballe

Re: Ejercicio 14 parte d)

de Nicolas Alejandro Scolaro Ribero -
Si, efectivamente es una T, me equivoque escribir la ecuación. Entiendo perfectamente lo que dices acerca de los vectores, pero no me doy cuenta con certeza cuándo utilizar la expresión completa de T o la expresión solo con su módulo. ¿Lo anterior no tiene ninguna relación con el hecho de que se trate de un vínculo unilateral o bilateral? Muchas gracias por tu respuesta. Saludos
En respuesta a Nicolas Alejandro Scolaro Ribero

Re: Ejercicio 14 parte d)

de Nicolas Alejandro Scolaro Ribero -
Otra cosa más, por definición la fricción siempre va a depender del módulo de la normal, por lo que me surge otra duda más de por qué en la solución de este problema (solución ej.1 - primer parcial 17 de mayo del 2014) ni siquiera hace el módulo de la normal para sustituirla en la fricción, sino que la sustituye así no más
En respuesta a Nicolas Alejandro Scolaro Ribero

Re: Ejercicio 14 parte d)

de Nicolás Casaballe -

Hay que aclarar varios aspectos:

- Le llamamos fuerza de reacción a la fuerza que aparece cuando dos cuerpos están en contacto (cada cuerpo ejerce una fuerza de reacción sobre el otro).

- La fuerza de reacción la pensamos como la suma de una componente normal, perpendicular a la superficie, y una componente tangencial que resulta ser la fuerza de fricción.

- Decimos que hay un vínculo unilateral cuando un cuerpo queda situado sobre la superficie del otro, de tal manera que el contacto se mantiene. Una de las cosas que destacamos es que ese cuerpo no puede pasar a través de la superficie, aunque sí podría abandonar ésta eventualmente. Esta situación corresponde a decir que la fuerza normal es siempre saliente desde el punto de vista de la superficie que la está ejerciendo (empuja hacia afuera).


- El vínculo es bilateral si el cuerpo queda sobre la superficie del otro y además la fuerza de reacción se ocupa de esta relación se mantenga: no solamente impide que el cuerpo atraviese la superficie, sino que además impide que abandone la superficie. Para ello, la fuerza normal puede llegar a ser entrante a la superficie que la ejerce. Eso va a depender del resto de las fuerzas que aparecen sobre los cuerpos y de qué forma se mueven.


- El sentido de la fricción no se relaciona directamente con el sentido de la normal. En cambio, la fricción aparece en dirección opuesta al desplazamiento relativo entre las superficies. Aquí hace falta distinguir la situación dinámica de la situación estática. Si las superficies se mueven entre sí, la fuerza de rozamiento es dinámica (o cinética) y tiene la dirección opuesta a la velocidad relativa entre ellas. Si las superficies no deslizan entre ellas, la fuerza de rozamiento es estática y su dirección va a depender de las demás fuerzas del sistema, y va a apuntar en un sentido tal que se mantenga la situación estática.

- El valor de la fuerza de rozamiento responde a leyes empíricas, no a una definición. Para el contacto entre superficies sólidas, estamos empleando la Ley de Coulomb, que surge de generalizar las observaciones encontradas a partir de múltiples experimentos. De acuerdo con esta ley, se cumple que

  • En el caso dinámico, el módulo de la fricción vale 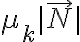\mu_k |\vec N|, donde 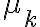\mu_k es un coeficiente de fricción dinámico constante, que depende de las superficies.
  • En el caso estático, el módulo de la fricción puede variar desde cero hasta un valor máximo 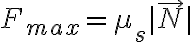F_{max} = \mu_s |\vec N|, donde 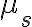\mu_s es un coeficiente de fricción estático constante, que depende de las superficies.

En otras palabras: la fuerza de fricción es mayor cuanto más apretados entre sí están los cuerpos.

- Al resolver un problema con una fuerza de rozamiento estática, su valor queda determinado a partir del valor de las demás fuerzas. Eso es lo que sucede en el ejercicio que mencionas. Lo que se hace es

(1) Asumir que se mantiene la situación estática y a partir de ahí calcular todas las fuerzas del sistema,

(2) Una vez halladas las fuerzas, verificar que efectivamente se cumple la condición 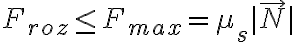F_{roz} \leq F_{max} = \mu_s |\vec N|.

(3) Si suceder que no se cumple la condición en (2), hay que resolver nuevamente el sistema, pero ahora considerando una fuerza de rozamiento dinámica.


Estos temas de las fuerzas de reacción lo vamos a seguir viendo en muchos de los problemas de nuestro curso, así que no va a faltar oportunidad de practicar. No dudes en consultar nuevamente si tienes más preguntas.

Saludos,
NC