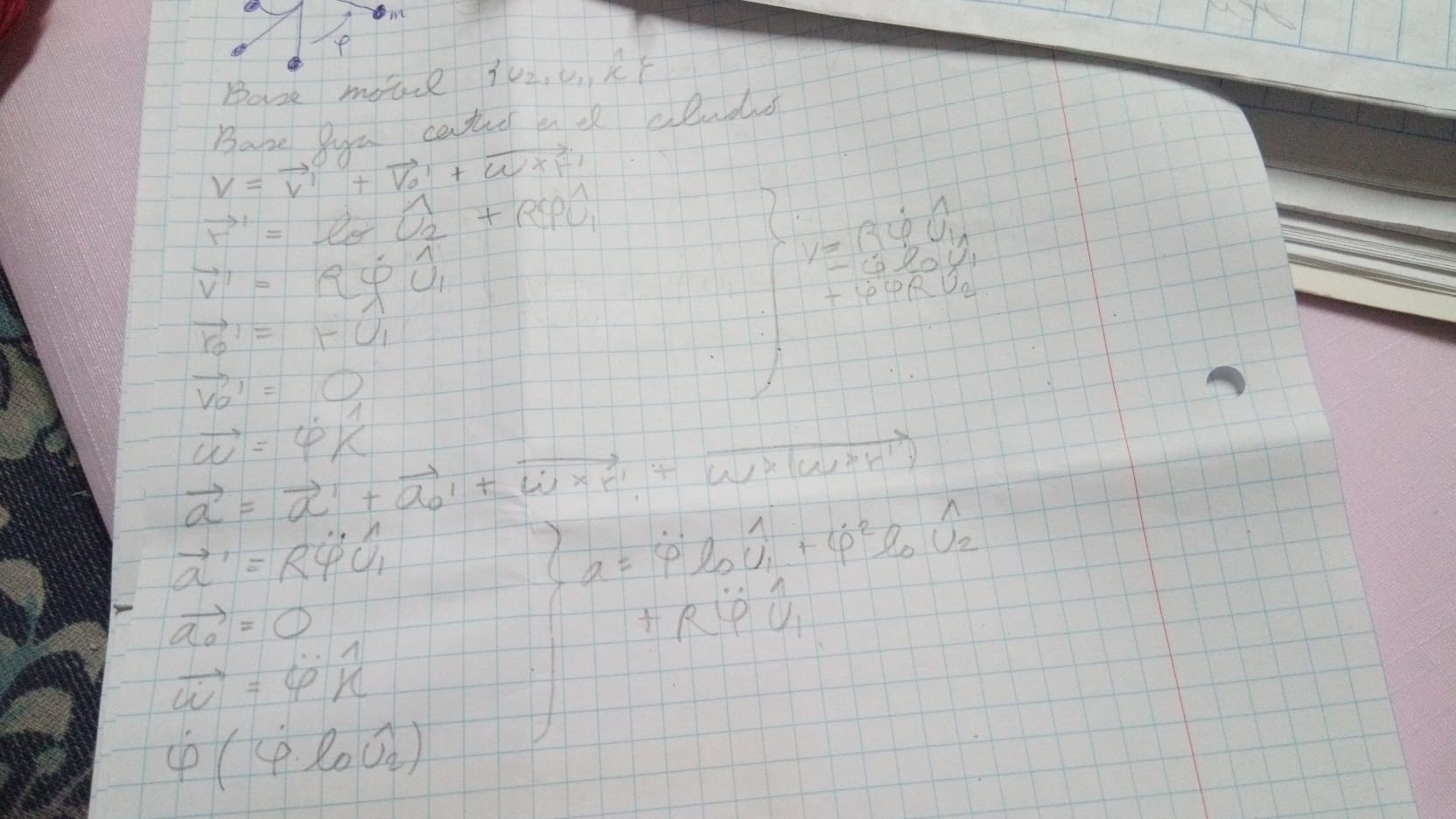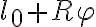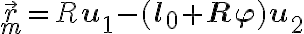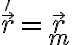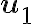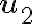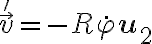15

15

de Nataly Melanie Ruber Maimo -
Número de respuestas: 7

hola tengo una duda respecto al 15, no sé bien cómo elegir las bases; lo que se me ocurre es tomar la base móvil u2, u1, k, con centro en la partícula y una base fija con centro en el cilindro, estaría bien? el ejercicio no me termina de quedar y capaz es por eso, y también tengo de duda si habría que usar en la posición r*fi, o sea arco de circunferencia, puesto que se desenrolla pero no sé

gracias

En respuesta a Nataly Melanie Ruber Maimo

Re: 15

de Ivan Ezequiel Rivero Tabarez -
Hola, lo que planteaste sobre las bases está bien, imagino que tus errores deben estar en las cuentas. A mi en lo personal me gusta tomar orígenes como puntos fijos, en este caso el centro del cilindro y a partir de ahí hago mis cuentas.
Sobre lo otro que comentaste, la masita se está enrollando, por ende vas a tener un término de R*phi en la dirección de u_2. El signo de ese término te recomiendo que lo veas imaginando donde está la partícula en t=0 y donde está en un instante posterior.
Espero haberte ayudado
En respuesta a Ivan Ezequiel Rivero Tabarez

Re: 15

de Nataly Melanie Ruber Maimo -
hola creo que sigo teniendo algo mal, o sea bajo mi idea, r' tendría que ser 0 pues tomo la base móvil en la partícula, v' también 0. ro' sería Rfi_u2 +Ru1, porque sería la distancia entre esa base y el centro del cilindro me parece, y vo': Rfi punto_u2, y ta el w sería fi punto k, que igual el término wxr' da 0. Pero lo que me dio no da, no sé qué hay mal pero si hay error debe estar en ro'. Me da la impresión que debería haber algún término lo_u2 pero no logro que quede :(
En respuesta a Nataly Melanie Ruber Maimo

Re: 15

de Ivan Ezequiel Rivero Tabarez -
Si, el error está en r_o'. Acordate que la posición se tiene que cumplir en todo instante de tiempo. Si yo tomo r_o'=Rphi punto_u2+R_u1, entonces en el instante inicial (phi=0) te quedaría que r_o'=R_u1 y no tendría sentido, pues en ese instante la masa no está pegada al cilindro según la letra, se entiende? Cuando phi es 0 (o mejor dicho, en un entorno del instante inicial), el largo de la cuerda tiene un valor, el cual coincide con l_o. Tu posición no estaba del todo mal, solo que en u_2 te faltó agregar la distancia inicial, el termino Rphi es el término asociado al enrollamiento del hilo
En respuesta a Ivan Ezequiel Rivero Tabarez

Re: 15

de Guzman Hernandez -
Hola,
Una aclaración clave: hay una diferencia conceptual entre base de versores y sistema de coordenadas.
Una base de versores es simplemente tres vectores unitarios ortogonales en el espacio. No tienen origen (uno puede poner el origen de estos vectores en cualquier lado, lo único que importa son sus direcciones y sentidos).
Un sistema de coordenadas queda definido por un origen de coordenadas y tres direcciones que el sistema ve fijas.

Otra aclaración importante: en cualquier sistema de coordenadas uno puede usar la base de versores que quiera. Lo único que hay que tener en cuenta es que algunas bases pueden ser móviles en un sistema y fijas en otro y viceversa.

Un consejo general: usualmente, tomar un sistema de coordenadas con origen en la posición de la partícula cuyo movimiento quieren escribir no sirve para nada. Mi sugerencia para Nataly es que rehagas ese ejercicio no tomando un sistema de coordenadas con origen en la posición de la partícula.

Saludos
Guzmán
En respuesta a Guzman Hernandez

Re: 15

de Nataly Melanie Ruber Maimo -

parece ser que llegué porque la aceleración me da correcta, pero hay alguna relación que se me está pasando por encima porque la velocidad no me da, hay dos términos allí que se me anulan pero no tengo ni idea porqué :( 


En respuesta a Nataly Melanie Ruber Maimo

Re: 15

de Nicolás Casaballe -

Hola, Nataly. Hay que revisar el planteo. La posición relativa de la partícula en tu sistema no está bien planteada. Eso hace que la velocidad relativa que obtienes no sea correcta.

Fijate en el siguiente esquema (le llamo R al radio para evitar confusiones con la posición). La longitud de la parte del hilo que está separado del cilindro es 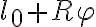l_0 + R \varphi.


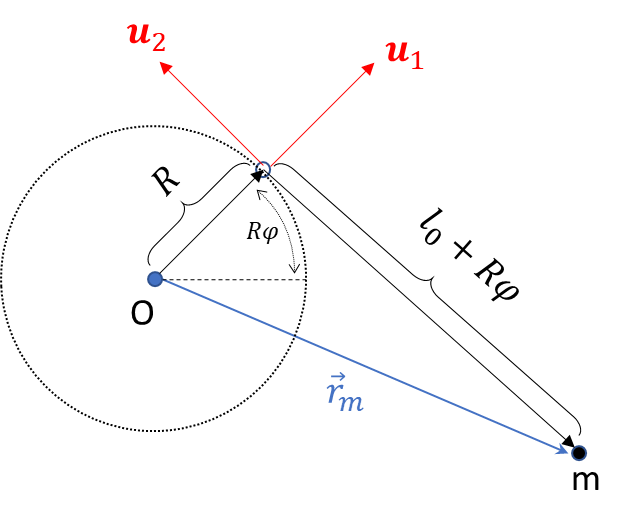
Tomando eso en cuenta, el vector que va desde el centro del cilindro hasta la partícula es

\vec r_m = R \mathbf u _1 - (l_0 + R\varphi) \mathbf u _2 .

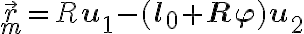Como elegiste un sistema móvil con ese origen, tu posición relativa es precisamente ese vector:

\vec r' = \vec r_m

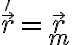
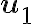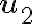La particularidad es que, vistos desde tu sistema móvil, los vectores \mathbf u_1 y \mathbf u_2 son constantes. Entonces, la velocidad relativa (calculada en ese sistema) queda

\vec v' = - R \dot \varphi \mathbf u _2

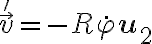
Revisa por favor estas cuentas, a ver si estás de acuerdo, y vuelve a calcular los términos del teorema de Roberval, a ver qué te dan ahora. Contanos qué tal te va.

Saludos,
NC