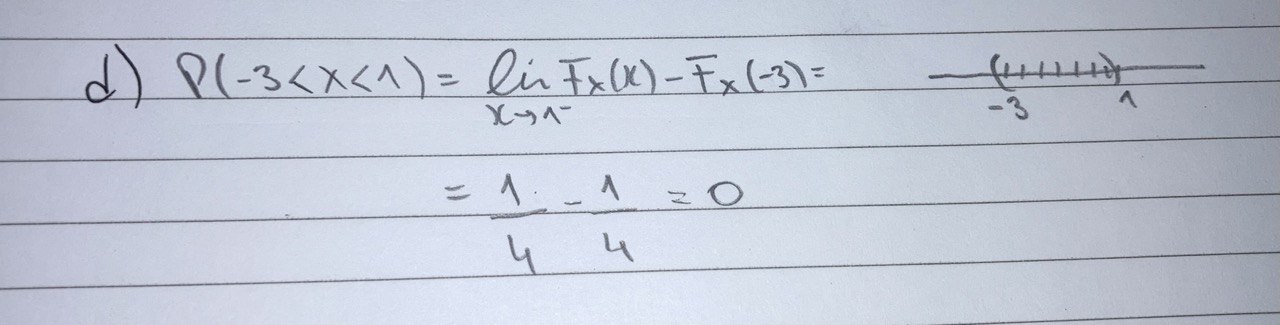Buenos dias. En este ejercicio el resultado me dio cero. Que me parece que tiene sentido por las propiedades que dimos en clase. Pero me esta costando hacerme ideas de la funcion de distribución.
Se me hace raro el concepto de "la probabilidad de que X grande esté en un intervalo".
Además, por qué si la X grande esta acotada en un intervalo donde la funcion de distribución vale siempre lo mismo, la "probabilidad de que X grande esté en ese intervalo" vale cero?. Gracias!