CDIVV - 1S: Ejercicio 2 parte b y c

Buenas, en la parte b de este ejercicio vi que la solución es -i pero a mí me está dando i y no logro darme cuenta que estoy haciendo mal. En la parte c quede trancado y no se cómo seguir el ejercicio, podrían ayudarme?. Saludos.

Re: Ejercicio 2 parte b y c

de Geronimo De Leon Ramirez - martes, 8 de marzo de 2022, 15:43

Buenas.

En la parte b), venías haciendo las cuentas bien, pero fijate que en el denominador, cuando hacés

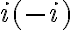$i(-i)$ , como bien pusiste, es el módulo de

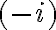$(-i)$ al cuadrado, o sea

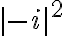$|-i|^2$ . El módulo, o radio de

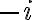$-i$ es 1, no -1. El módulo siempre es un número real no negativo, y aunque hubieras puesto que era -1, al elevarlo al cuadrado seguía siendo 1. Al final te queda

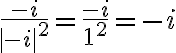$\frac{-i}{|-i|^2}=\frac{-i}{1^2}=-i$ . Fijate que haciendo la cuenta directamente,

$i(-i)=(-1)ii=(-1)(i)^2=(-1)(-1)=1$ .

En la parte c), venís perfecto. La parte de abajo es el módulo de

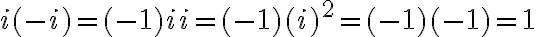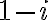$1-i$ al cuadrado, graficá el complejo

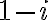$1-i$ y fijate cuál es su módulo, o calculalo directamente:

$\sqrt{1^2+(-1)^2}=\sqrt{2}$ .

Re: Ejercicio 2 parte b y c

de Luciano Umpierrez Garcia - martes, 8 de marzo de 2022, 18:33

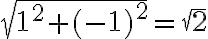Gracias por la ayuda. Me termino quedando así pero no logro darme cuanta como pasarlo a la forma polar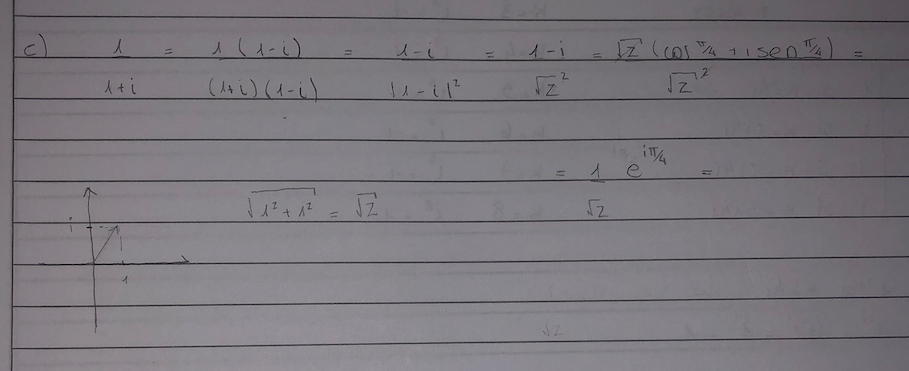

Re: Ejercicio 2 parte b y c

de Geronimo De Leon Ramirez - martes, 8 de marzo de 2022, 23:52

Esa es la forma polar. Supongo que te referías a la forma binómica, que ya la tenías un poquito antes.

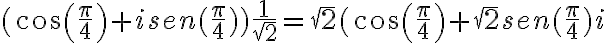$(cos(\frac{\pi}{4})+isen(\frac{\pi}{4}))\frac{1}{\sqrt{2}}=\sqrt{2}(cos(\frac{\pi}{4})+\sqrt{2}sen(\frac{\pi}{4})i$ , diferenciando quién es la parte real y quién la parte imaginaria. Para que quede más reducido, usás que

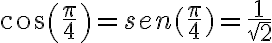$cos(\frac{\pi}{4})=sen(\frac{\pi}{4})=\frac{1}{\sqrt2}$ y te queda

$\frac{1}{2}+\frac{1}{2}i$ .

Otro camino es, ya que tenés la forma polar, usar trigonometría para hallar lo que te falta (sabés que la hipotenusa es el radio y que los catetos son la parte real y la parte imaginaria, y tenés un ángulo).