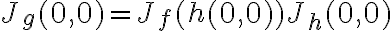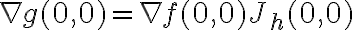Hola. La idea de este ejercicio es utilizar la regla de la cadena: podemos ver a  como la composición de la función
como la composición de la función  con
con  , es decir,
, es decir, 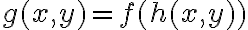 . Entonces la regla de la cadena nos dice que:
. Entonces la regla de la cadena nos dice que:
Observando que 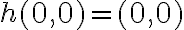 y que el Jacobiano de una función de
y que el Jacobiano de una función de 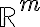 a
a 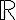 es el gradiente, tenemos que:
es el gradiente, tenemos que:
El jacobiano de  lo podés calcular a partir de la fórmula de
lo podés calcular a partir de la fórmula de  . Una vez que tengas el gradiente de
. Una vez que tengas el gradiente de  , fijate que la derivada direccional respecto a la dirección
, fijate que la derivada direccional respecto a la dirección 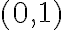 es la derivada parcial respecto de
es la derivada parcial respecto de  , es decir, es la segunda entrada del vector gradiente.
, es decir, es la segunda entrada del vector gradiente.
Saludos