Hola buenas, no me salió este ejercicio, aplique el cambio de variable de esféricas, y llegue a que ρ va de √2 a 1/sen(φ), φ de 0 a π/4 y θ de 0 a π/2, quedándome la función a integrar ρ^3sen(φ)cos(φ), luego de integrar por primera vez, llego a una función que no converge. Me podrían ayudar, muchas gracias
Hola. Viste que el ejercicio sugiere hacer cambio de variable a cilíndricas, y vos creo que hiciste un cambio a esféricas. Con el cambio a cilíndricas (
, 
, 
) debería quedarte más fácil de integrar.
Saludos
Buenas,
Probando con el cambio de variable a cilíndricas no logre llegar al resultado, los nuevos limites de integración me quedaron que z va de 0 a √(2-ρ^2), ρ de 0 a 1 y θ de 0 a π/2, integrando zρ, y llego a un resultado de 3π/16, no se donde podría llegar a estar el error en cuanto a los limites.
Probando con el cambio de variable a cilíndricas no logre llegar al resultado, los nuevos limites de integración me quedaron que z va de 0 a √(2-ρ^2), ρ de 0 a 1 y θ de 0 a π/2, integrando zρ, y llego a un resultado de 3π/16, no se donde podría llegar a estar el error en cuanto a los limites.
Hola. Los límites de integración en 
deberían ser 0 y 
. Eso se puede ver de la condición 
: en cilíndricas esa condición queda 
y como 
, eso se cumple si 
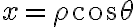
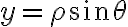
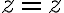
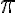
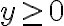
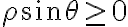
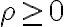
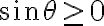
(es decir, si ![\theta \in [0,\pi]](https://eva.fing.edu.uy/filter/tex/pix.php/6cc8f3093bbf7ae79a654c78aee98bfb.png "\theta \in [0,\pi]")
).
Saludos
Ahora si logre llegar, muchas gracias por la respuesta, saludos