Ejercicio 4, examen Diciembre 2018

Ejercicio 4, examen Diciembre 2018

de Martin Nicolas Ripoll Camejo -
Número de respuestas: 4

Buenas, 

Estoy teniendo problemas con el siguiente ejercicio:


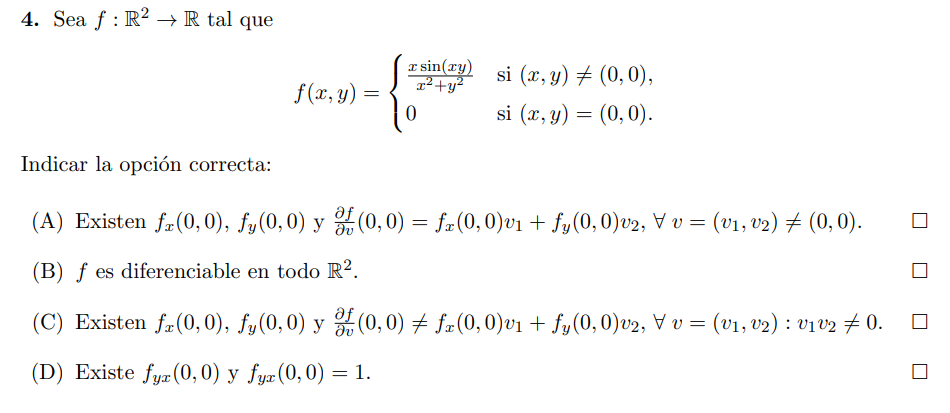
Calcule las derivadas parciales en (0,0) y ambas valen 0. Por otra parte, calcule el valor de las derivadas direccionales en el mismo punto y también valen 0 para todo vector v tal que v_1*v_2 sea distinto de 0.
Visto esto, la respuesta que mas se aproxima a mis resultados seria la C, que es la correcta, pero sin embargo no entiendo por qué la combinación lineal de las derivadas parciales sería distinta al valor de las derivadas direccionales para todo v. Agradecería que me aclaren esa parte de la afirmación.

Saludos.


En respuesta a Martin Nicolas Ripoll Camejo

Re: Ejercicio 4, examen Diciembre 2018

de Amalia Lucia Balestrazzi Silveira -
Hola,
A mi las derivadas direccionales en (0,0) me dieron (v_2*v_1^2)/(v_1^2+v_2^2), que es distinto de cero si v_1*v_2 es distinto de cero.
Esa derivada direccional hay que calcularla como el límite del cociente incremental en la dirección del vector v, no se puede calcular como la combinación lineal de las parciales porque f no es diferenciable.

Saludos!
En respuesta a Amalia Lucia Balestrazzi Silveira

Re: Ejercicio 4, examen Diciembre 2018

de Jessica Sista Arriola -
¿f no seria diferenciable porque el resto da cos( \theta ? Pregunto porque eso fue lo que me dio a mi pero no se si es correcto.
Muchas gracias.
En respuesta a Jessica Sista Arriola

Re: Ejercicio 4, examen Diciembre 2018

de Amalia Lucia Balestrazzi Silveira -
Buenas,
Supongo que cuando decis que el resto te dio cos(θ) te referis al límite de r(x,y) sobre la norma de (x,y). No me dio lo mismo, pero también al pasarlo a polares me dio dependiende de theta, por lo que concluyo que el límite no existe y f no es diferenciable.
Te adjunto mis cuentas por si te sirve, pero verificalo porque puede haber algún error en mis cuentas.

Saludos

ej4