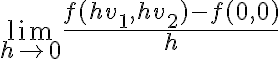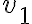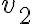Hola, estaba viendo la solución de este ejercicio y me surgió una duda, vi que probaron que las derivabas parciales existían y luego fueron directo a probar si era diferenciable, al serlo ahí concluía el ejercicio. Pero mi duda esta en que si no lo hubiera sido, como pruebo que las derivadas direccionales existen, porque con lo hecho en la solución me quedaría entre la opción C y D
Hola. En ese caso tendrías que estudiar las derivadas direccionales usando la definición, es decir, estudiando el límite del cociente incremental 
, discutiendo según 
y 
(para estudiar la derivada en todas las direcciones posibles).
Saludos
Podrías ver directamente si existen las derivadas direccionales usando la definición, al igual que se hace para las derivadas parciales. Habría que tomar un vector v genérico y plantear el límite del cociente incremental (f(hv)-f(0))/h.
En respuesta a Mariana Morales Sanabria
Re: Ejercicio 4 examen diciembre 2021
Para probar q las derivadas direccionales existen tenés q probar el límite ese q tenés que poner un vector genérico , como haces en las parciales con el (10)y (01) en las direccionales pones un vector (xy) y al igual q en las parciales calculas el límite si existe y es finito. Creo q es así. Pero por las dudas espera la contestación d algún profe