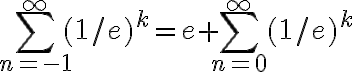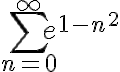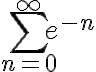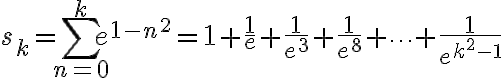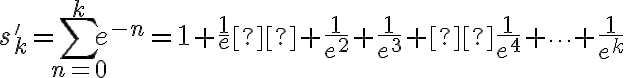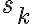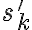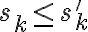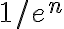CDIVV-2S: Ej 1 examen diciembre 2021

Buenas,

Vi la solución del ejercicio y me quedó claro cómo lo resolvieron. Quería saber si la forma en que lo resolví yo es válida. Mi respuesta fue correcta pero al ser verdadero/falso eso no dice mucho.

El ejercicio en cuestión es:

ej1

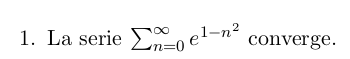
En la solución se usa el criterio de la raíz.

A mi lo que se me ocurrió es hacer un cambio de variable 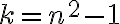$k=n^2-1$ , y consideré la sucesión:

$\sum_{n=-1}^{\infty} (1/e)^k = e+ \sum_{n=0}^{\infty} (1/e)^k$ , la cual es convergente.

La serie que nos interesa es una subsucesión de esta última serie, entonces también es convergente.

¿Este razonamiento es correcto?

Gracias

Re: Ej 1 examen diciembre 2021

de Bernardo Marenco - lunes, 7 de febrero de 2022, 10:58

Hola. La idea está bien, aunque hay un pequeño detalle: las sucesión asociada a la serie $\displaystyle \sum_{n=0}^{\infty} e^{1-n^2}$ estrictamente no es una subsucesión de la asociada a $\displaystyle \sum_{n=0}^{\infty} e^{-n}$ (aunque se le parece bastante). Fijate que la sucesión de sumas parciales asociada a la primera serie es:

$\displaystyle s_k = \sum_{n=0}^{k} e^{1-n^2} = 1+\frac{1}{e} + \frac{1}{e^3} + \frac{1}{e^8} + \dots + \frac{1}{e^{k^2-1}}$

mientras que la de la segunda serie es

$\displaystyle s'_k = \sum_{n=0}^{k} e^{-n} = 1+\frac{1}{e} +\frac{1}{e^2}+ \frac{1}{e^3} + \frac{1}{e^4} + \dots + \frac{1}{e^{k}}$

Entonces en $s_k$ aparecen algunos sumandos de $s_k'$ , por lo que $s_k \leq s_k'$ como $s_k'$ converge, por comparación $s_k$ converge. Aunque lo parece, en realidad $s_k$ no es una subsucesión de $s_k'$ porque en cada término de $s_k'$ aparecen sumadas todas las potencias de $1/e^n$ , mientras que en los de $s_k$ eso no sucede (por ejemplo, el término $1/e^2$ nunca aparece).

Saludos