Foro de Ejercicios fuera de los Prácticos

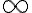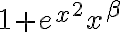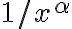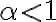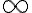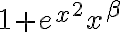Hola. Como bien dijiste, hay que separar la impropia entre lo que pasa en 0 y lo que pasa en $\infty$. En 0 el término $1+e^{x^2}x^\beta$ es equivalente a 1, por lo que la impropia es equivalente a $1/x^\alpha$, que converge si $\alpha < 1$. En $\infty$, $1+e^{x^2}x^\beta$ es equivalente a 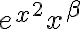$e^{x^2}x^\beta$, así que la impropia es equivalente a 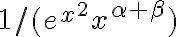$1/(e^{x^2}x^{\alpha+\beta})$. La impropia de esa función en 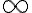$\infty$ es siempre convergente, porque la exponencial es de mayor orden que el polinomio, y la impropia de 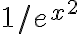$1/e^{x^2}$ converge.

Saludos