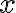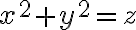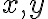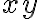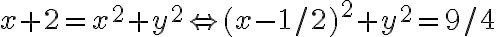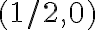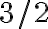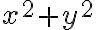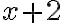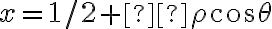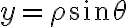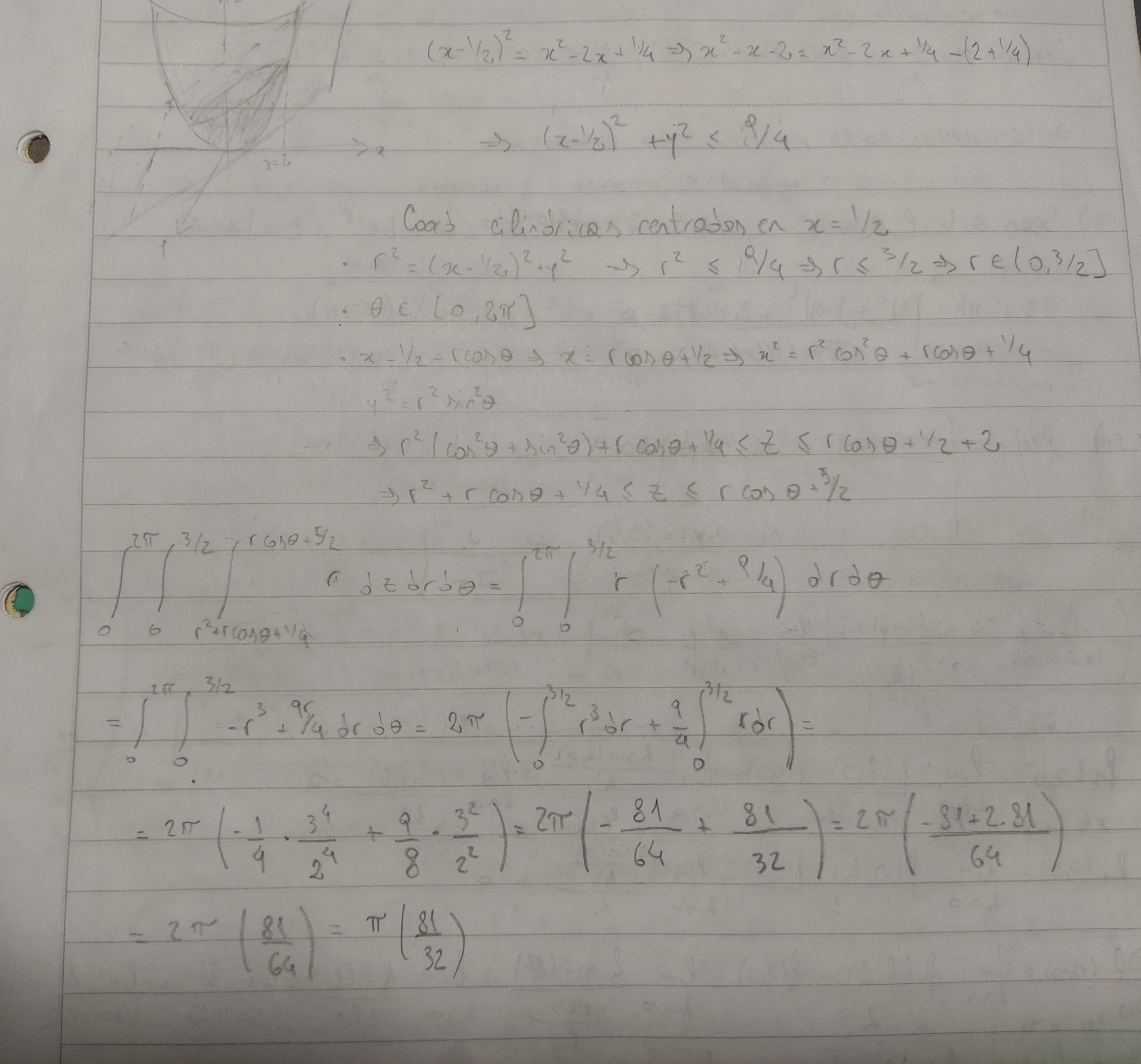Buenas, para este no me pareció muy evidente cómo quedaban los límites de integración al pasar a cilíndricas así que traté de hacerlo en coordenadas cartesianas.  es fácil de acotar porque está dado por la letra,
es fácil de acotar porque está dado por la letra, ![z \in [x^2 + y^2, x+2] z \in [x^2 + y^2, x+2]](https://eva.fing.edu.uy/filter/tex/pix.php/cad8e15371a9cd5b5db6913ce0a20f33.gif) . Para acotar x e y dije:
. Para acotar x e y dije:
Cuando  es máximo/mínimo, y=0 y entonces tengo que
es máximo/mínimo, y=0 y entonces tengo que 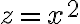 y
y 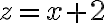 , entonces
, entonces 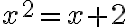 , por lo que
, por lo que ![x \in [-1,2] x \in [-1,2]](https://eva.fing.edu.uy/filter/tex/pix.php/9f9a9a9a8224a6838e9ecbc003704104.gif) .
.
De la misma manera, dije que cuando  es máximo/mínimo, x=0, y me quedó que
es máximo/mínimo, x=0, y me quedó que ![y \in [-\sqrt{2},\sqrt{2}] y \in [-\sqrt{2},\sqrt{2}]](https://eva.fing.edu.uy/filter/tex/pix.php/20dd5a362b7c341641b747cb0a3b0fda.gif) .
.
Esto me dio 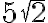 , que no es ninguna de las opciones. Este resultado lo verifiqué y está bien, por lo que el error debe estar al acotar x y/o y. ¿Me pueden ayudar a encontrar el error?
, que no es ninguna de las opciones. Este resultado lo verifiqué y está bien, por lo que el error debe estar al acotar x y/o y. ¿Me pueden ayudar a encontrar el error?
(no se por qué no me quedan bien los símbolos en latex)
Adjunto la letra del ejercicio
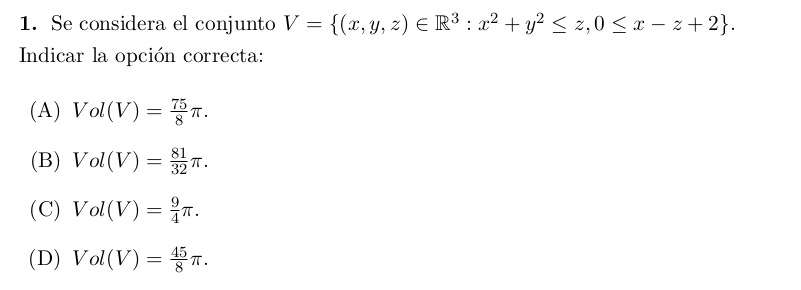
Gracias


![x \in [-1,2] x \in [-1,2]](https://eva.fing.edu.uy/filter/tex/pix.php/92b837238a79b8c5d1684c852a4bb489.gif)
![y \in [-\sqrt{2}, \sqrt{2}] y \in [-\sqrt{2}, \sqrt{2}]](https://eva.fing.edu.uy/filter/tex/pix.php/efec59a0faaec78f2c49350e9b236358.gif)