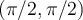Buenas, entiendo la forma de resolución del ejercicio, lo que no entiendo es porque se ignora el 1 del punto (pi/2,pi/2,1). La componente z no se toma en cuenta, porque?
Re: Segundo parcial 2019. Ejercicio 2 versión 1
Re: Segundo parcial 2019. Ejercicio 2 versión 1
Re: Segundo parcial 2019. Ejercicio 2 versión 1
Hola. El plano tangente está definido para un punto del gráfico de la función, es decir, es un plano que vive en 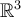 . Si yo quiero calcular el plano tangente al gráfico de la función en un punto de coordenadas
. Si yo quiero calcular el plano tangente al gráfico de la función en un punto de coordenadas 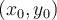 , voy a buscar la ecuación de un plano que pase por el punto de
, voy a buscar la ecuación de un plano que pase por el punto de 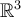 de coordenadas
de coordenadas 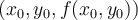 . Entonces, al pedirnos el plano tangente en
. Entonces, al pedirnos el plano tangente en  lo que nos están diciendo es que
lo que nos están diciendo es que  (cosa que ya sabemos por la ecuación que define a la función).
(cosa que ya sabemos por la ecuación que define a la función).
Por otro lado, la ecuación del plano tangente es  . Para la función en particular de este ejercicio se cumple que
. Para la función en particular de este ejercicio se cumple que  , entonces la ecuación queda solo
, entonces la ecuación queda solo  . Pero eso es cierto solo porque las derivadas parciales se anulan en el punto. Eso no tiene por qué ser cierto para una función
. Pero eso es cierto solo porque las derivadas parciales se anulan en el punto. Eso no tiene por qué ser cierto para una función  cualquiera (de hecho, si fuese cierto siempre los planos tangentes siempre serían paralelos al plano
cualquiera (de hecho, si fuese cierto siempre los planos tangentes siempre serían paralelos al plano 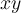 ). Creo que lo que confunde es que en la letra de la prueba dice
). Creo que lo que confunde es que en la letra de la prueba dice 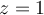 . Supongo que hay un error ahí, la letra debería decir
. Supongo que hay un error ahí, la letra debería decir 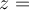 (y que cada uno completara el lado derecho de la igualdad con la ecuación que correspondiera).
(y que cada uno completara el lado derecho de la igualdad con la ecuación que correspondiera).
Saludos