Buenas, en el punto (0,0) de esta función las derivadas parciales no dan ambas 0? Y como son continuas en el punto debería ser diferenciable como dice la tercera proposición del repartido con las soluciones? O sea, qué parte de esa proposición no se estaría cumpliendo? Porque la solución dice que no es diferenciable en ese punto. Gracias
Hola Andrés
Efectivamente ambas derivadas parciales existen y son nulas en el (0,0). Lo que no es verdad es que sean continuas. Podés fijarte por ejemplo que en la región comprendida entre las parábolas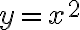
e 
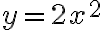, cuando 
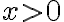se tiene 
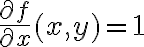y si 
se tiene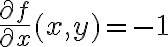 
. Por lo que en 
no es continua (en un entorno tan chico como quieras de (0,0) hay puntos para los cuales la derivada parcial vale 1, -1 o 0).
Para probar que no es diferenciable basta con ir a la definición de diferenciabilidad en un punto (el candidato a diferencial en (0,0) sería la transformación lineal nula).
Efectivamente ambas derivadas parciales existen y son nulas en el (0,0). Lo que no es verdad es que sean continuas. Podés fijarte por ejemplo que en la región comprendida entre las parábolas
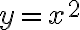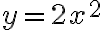e , cuando 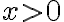se tiene 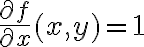y si se tiene 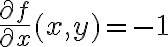. Por lo que en no es continua (en un entorno tan chico como quieras de (0,0) hay puntos para los cuales la derivada parcial vale 1, -1 o 0).Para probar que no es diferenciable basta con ir a la definición de diferenciabilidad en un punto (el candidato a diferencial en (0,0) sería la transformación lineal nula).
Perfecto Favio, gracias.