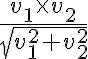 , y en la solución dice que las únicas derivadas
direccionales que existen son según (λ, 0) o (0, λ). Lo que no estaría entendiendo es por qué no existiría la derivada según (1,1) por ejemplo, basándome en el limite que me dio.
, y en la solución dice que las únicas derivadas
direccionales que existen son según (λ, 0) o (0, λ). Lo que no estaría entendiendo es por qué no existiría la derivada según (1,1) por ejemplo, basándome en el limite que me dio.Muchas gracias.
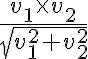 , y en la solución dice que las únicas derivadas
direccionales que existen son según (λ, 0) o (0, λ). Lo que no estaría entendiendo es por qué no existiría la derivada según (1,1) por ejemplo, basándome en el limite que me dio.
, y en la solución dice que las únicas derivadas
direccionales que existen son según (λ, 0) o (0, λ). Lo que no estaría entendiendo es por qué no existiría la derivada según (1,1) por ejemplo, basándome en el limite que me dio.Muchas gracias.
Buenas, me quedaron algunas dudas de este práctico y de este ejercicio en particular.
Entonces, para esta parte a), es correcto decir que existen las derivadas direccionales en el punto (0,0) para todas las direcciones de v= (v1,v2) con v1 y v2 reales?
Lo otro que no entiendo de la parte b) del mismo ejercicio, es porque en la solución dice que existen las derivadas direccionales para cualquier dirección.
Yo lo que plantee fue el limite en un punto generico del plano x=0, osea en (0,y0), para cualquier direccion v:
eso me dio como resultado 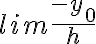 con h tendiendo a cero, que no existe porque yo es una constante.
con h tendiendo a cero, que no existe porque yo es una constante.
Fuera de ese plano si existe las derivadas, pero no entiendo porque en este plano existen, si estoy haciendo mal algún cálculo o razonando mal.
Saludos.
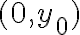 resulta
resulta