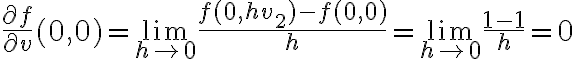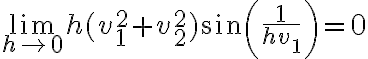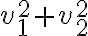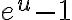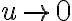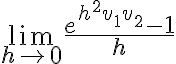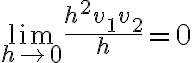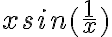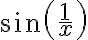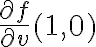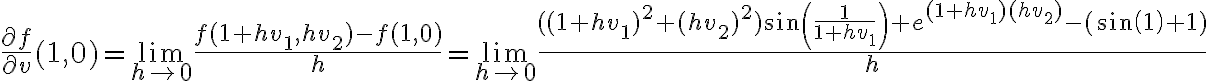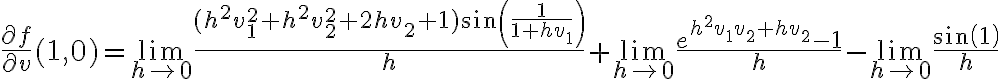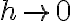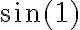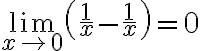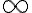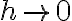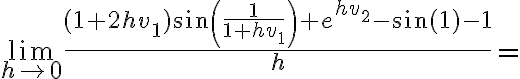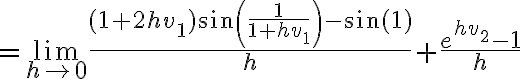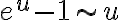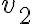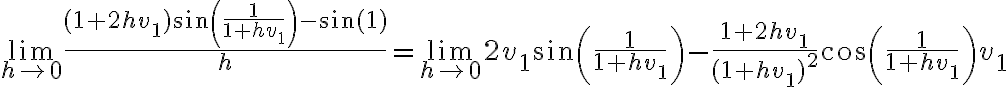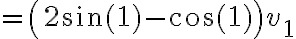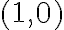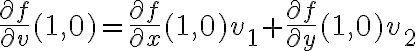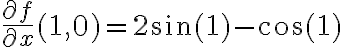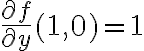Hola. Fijate que cuando 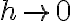 , en el numerador del primer término te queda
, en el numerador del primer término te queda 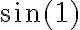 , así que eso tiende a un infinito "parecido" al del tercer término. Hay que tener cuidado al separar los límites como
sumas o restas de cosas, porque el límite de cada cosa puede no existir por separado pero el de la suma o resta sí. Tal vez el ejemplo más directo de que eso puede llevar a problemas es escribir
, así que eso tiende a un infinito "parecido" al del tercer término. Hay que tener cuidado al separar los límites como
sumas o restas de cosas, porque el límite de cada cosa puede no existir por separado pero el de la suma o resta sí. Tal vez el ejemplo más directo de que eso puede llevar a problemas es escribir
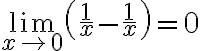
Ese límite es 0 porque lo que está adentro del límite es constante 0, pero si separo cada término se va a 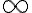 .
.
Acá lo que podés hacer es quedarte con lo de menor grado en  en lo que multiplica al seno y a la exponencial, ya que
en lo que multiplica al seno y a la exponencial, ya que 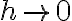 . Así llegás a algo como:
. Así llegás a algo como:
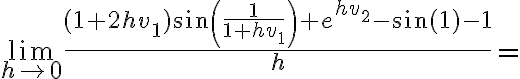
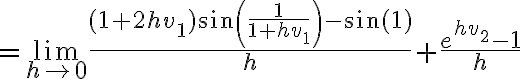
Acá separé las cosas en sumandos que tienen límite: fijate que usando que 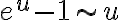 , el de la derecha tiende a
, el de la derecha tiende a 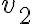 . Para el de la izquierda podemos usar L'Hopital:
. Para el de la izquierda podemos usar L'Hopital:
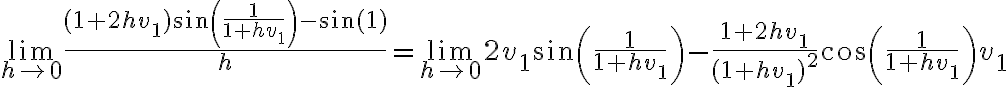
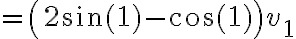
Así que la derivada direccional queda:  .
.
Algo interesante es que como  es diferenciable en
es diferenciable en 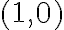 , en realidad ya sabemos que:
, en realidad ya sabemos que:
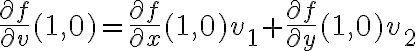
Usando que 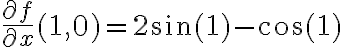 y que
y que 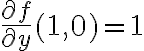 , hubiésemos llegado a lo mismo (pero sin evaluar ningún límite).
, hubiésemos llegado a lo mismo (pero sin evaluar ningún límite).
Saludos
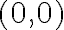 me queda que solo existen si la dirección es
me queda que solo existen si la dirección es 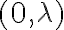 pero en la solu dice que existen para cualquier dirección.
pero en la solu dice que existen para cualquier dirección.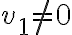 ,
,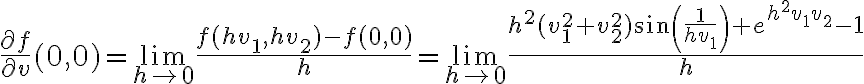
 no existe para ningún
no existe para ningún 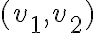
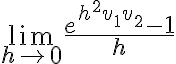 existe sólo si
existe sólo si 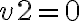
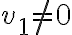 , no existen las derivadas direccionales.
, no existen las derivadas direccionales.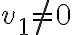 no existen las derivadas direccionales
no existen las derivadas direccionales 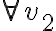
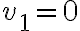 , existen
, existen 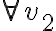 y valen 0.
y valen 0.