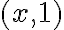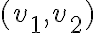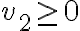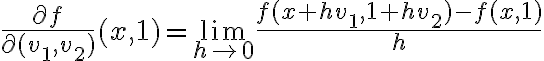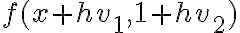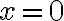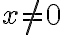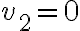Agradezco me puedan ayudar a ver dónde está mi error.
Mi razonamiento es el siguiente:
f es continua en todo
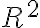 .
.Estudiemos el caso donde
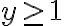 . Sea
. Sea  un vector genérico.
un vector genérico.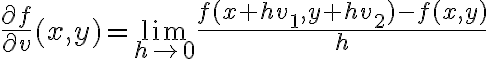
Luego,
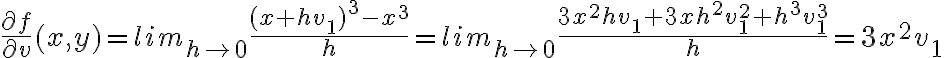 .
.En este caso, entiendo que este límite existe para todo
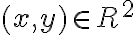 y para todo vector
y para todo vector  .
.Por otro lado, si
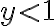 tenemos:
tenemos: 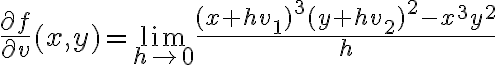
Desarrollando todo esto, dividiendo entre h y sacando los términos que conservan h (ya que h tiende a 0) nos queda
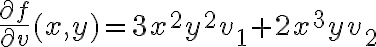
Donde también entiendo que existe para todo punto y para todo vector.