Buenas,
No entiendo, en general, la idea de cómo llegar a algo de la forma: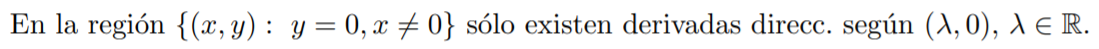
¿Me podrían dar una mano?
Saludos
Buenas,
No entiendo, en general, la idea de cómo llegar a algo de la forma: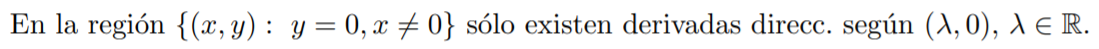
¿Me podrían dar una mano?
Saludos
Hola Joel. En la región abierta del plano donde  la función es un cociente de cosas que son diferenciables y en esa región el denominador no se anula, por lo que van a existir todas las derivadas direccionales en esos puntos.
la función es un cociente de cosas que son diferenciables y en esa región el denominador no se anula, por lo que van a existir todas las derivadas direccionales en esos puntos.
Si estudiás la continuidad sobre la recta 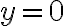 vas a ver que la función no es continua ahí: en los puntos con de la forma
vas a ver que la función no es continua ahí: en los puntos con de la forma 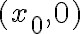 con
con 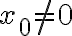 alcanza con mirar los límites direccionales en una dirección que no sea
alcanza con mirar los límites direccionales en una dirección que no sea 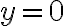 ; para el
; para el  podés estudiar qué pasa cuando te movés sobre la curva
podés estudiar qué pasa cuando te movés sobre la curva 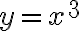 . Así que en esos puntos no puede ser diferenciable (ya que no es continua). Pero eso no nos dice nada sobre las derivadas direccionales, que igual podrían existir.
. Así que en esos puntos no puede ser diferenciable (ya que no es continua). Pero eso no nos dice nada sobre las derivadas direccionales, que igual podrían existir.
Si fijás un punto en esa recta, digamos 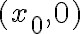 , entonces la derivada direccional según una dirección
, entonces la derivada direccional según una dirección 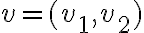 queda:
queda:
Si 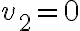 (lo que se corresponde con la dirección
(lo que se corresponde con la dirección 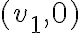 o
o 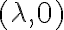 como lo pone la solución) entonces
como lo pone la solución) entonces 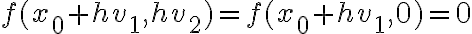 , por lo que la derivada en esa dirección existe y da 0. Si
, por lo que la derivada en esa dirección existe y da 0. Si 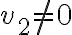 entonces
entonces  , así que la derivada direccional queda:
, así que la derivada direccional queda:
Cuando 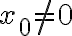 ese último límite tiende a
ese último límite tiende a 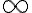 , por lo que no existen las derivadas direccionales en ese caso. Si
, por lo que no existen las derivadas direccionales en ese caso. Si 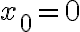 (es decir, el punto en el que estoy mirando las derivadas direccionales es el
(es decir, el punto en el que estoy mirando las derivadas direccionales es el  ), ese límite es 0, por lo
que ese es el único punto de la recta
), ese límite es 0, por lo
que ese es el único punto de la recta 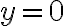 en el que existen todas las derivadas direccionales.
en el que existen todas las derivadas direccionales.
Saludos
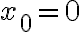 el limite es 0 porque en realidad lo de abajo tiende a 0, que no es lo mismo que valga 0, verdad? Porque yo lo pensaba como que me quedaba una indeterminación de 0/0 entonces no llegaba a la conclusión correcta.
el limite es 0 porque en realidad lo de abajo tiende a 0, que no es lo mismo que valga 0, verdad? Porque yo lo pensaba como que me quedaba una indeterminación de 0/0 entonces no llegaba a la conclusión correcta.Hola. Fijar 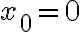 es equivalente a tomar el límite direccional según la dirección vertical. Que ese límite de 0 no te alcanza para probar que el límite exista (más en general, todos los límites direccionales pueden existir pero eso no implica que el límite en el punto exista). El problema del
es equivalente a tomar el límite direccional según la dirección vertical. Que ese límite de 0 no te alcanza para probar que el límite exista (más en general, todos los límites direccionales pueden existir pero eso no implica que el límite en el punto exista). El problema del  en este caso es que cualquier límite direccional te da 0 y eso no te alcanza para decir cuánto vale el límite. Por eso en una respuesta anterior sugería estudiar qué pasa sobre la curva
en este caso es que cualquier límite direccional te da 0 y eso no te alcanza para decir cuánto vale el límite. Por eso en una respuesta anterior sugería estudiar qué pasa sobre la curva 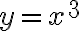 (spoiler: sobre esa curva el límite te da 1, entonces si por rectas da 0 y por esa curva da 1 podemos concluir que el límite en el punto no existe).
(spoiler: sobre esa curva el límite te da 1, entonces si por rectas da 0 y por esa curva da 1 podemos concluir que el límite en el punto no existe).
Saludos
 tanto por rectas como por curvas y observar las diferencias que tu explicaste, es válido también utilizar cambio de variable polar para demostrarlo?:
tanto por rectas como por curvas y observar las diferencias que tu explicaste, es válido también utilizar cambio de variable polar para demostrarlo?: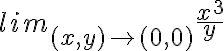 nos queda igual al
nos queda igual al 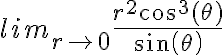 , donde se observa que
, donde se observa que 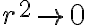 , pero
, pero 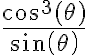 no está acotado. pues cuando
no está acotado. pues cuando 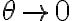 el cociente tiende a
el cociente tiende a 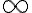
Hola. Que la parte angular no esté acotada no alcanza para probar que el límite no existe. La proposición que estás tratando de usar dice que si la parte angular está acotada y la radial tiende a 0, entonces el límite existe y da 0. No dice nada sobre qué pasa si esas hipótesis no se cumplen. En otras palabras: esa parte angular puede no estar acotada pero el límite igual podría existir.
Saludos