Mi duda surge con el ejercicio 7 a la hora de verificar si en el (0,0) la función es diferenciable o no. No logro comprender porque en la clase de practico a la hora de resolver su "diferenciabilidad" para la cual es necesario hallar su derivadas parciales, se utiliza la definicion de derivada y no se hace "directamente". Yo entiendo que el punto (0,0) es un punto "problematico" y por eso seria necesario utlilizar la definicion pero en el ejercicio 4.a por ejemplo, cuando piden hallar las derivadas parciales también en el punto (0,0) el cual era tambien un punto problematico, en esa funcion si se puede derivar "directamente" las parciales para luego hallar las direccionales.
Hola Agustín. Entiendo que estás preguntando por qué en el ejercicio 7, para hallar las derivadas parciales en  , no podés simplemente derivar respecto a
, no podés simplemente derivar respecto a  la fórmula
la fórmula 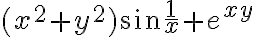 y luego hacer
y luego hacer 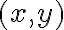 tender a
tender a  . El problema con eso es que estás asumiendo que la función "derivada parcial según
. El problema con eso es que estás asumiendo que la función "derivada parcial según  " es continua en
" es continua en  , cosa que no sabés si es cierta (porque de hecho no sabés ni siquiera si existe en (0,0)). Digo que estás usando que es continua porque fijate el procedimiento que querés seguir:
, cosa que no sabés si es cierta (porque de hecho no sabés ni siquiera si existe en (0,0)). Digo que estás usando que es continua porque fijate el procedimiento que querés seguir:
- Derivando respecto a
 la fórmula
la fórmula 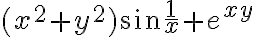 , hallás la función
, hallás la función 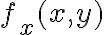 para aquellos puntos donde
para aquellos puntos donde 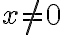 .
. - Tomás límite de esa función cuando
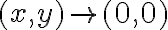 y decís que eso es
y decís que eso es 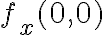 . Fijate que lo que estás diciendo es que
. Fijate que lo que estás diciendo es que 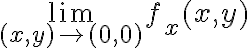 tiene que ser igual a
tiene que ser igual a 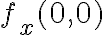 , es decir, que
, es decir, que 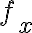 es continua en
es continua en  (cosa que nada te asegura que sea cierto, y de hecho en este ejercicio no lo es).
(cosa que nada te asegura que sea cierto, y de hecho en este ejercicio no lo es).
Por lo tanto, la forma segura de hacerlo es mirar el cociente incremental en el punto para hallar la derivada parcial. Digo segura porque puede pasar (y eso capaz que es lo que pasa en el ejercicio 4a) que la derivada exista y sea continua, entonces ese procedimiento te lleva al resultado correcto. Pero si hacés eso en el ejercicio 7 vas a concluir (incorrectamente) que la derivada parcial respecto a  no existe, cuando sí existe (el tema es que no es continua).
no existe, cuando sí existe (el tema es que no es continua).
 no existe, cuando sí existe (el tema es que no es continua).
no existe, cuando sí existe (el tema es que no es continua).Saludos
Muchas gracias Bernardo, me quedo clarisimo ahora, un saludo!
