Buenas. Cuando yo paso todo a polares y el límite me converge a un número, o sea no depende de el ángulo, es suficiente para decir que converge a ese número o es como cuando hacemos con y=mx? Que si no depende de m no podemos afirmar nada. Gracias
Hola Juan
Fijar un ángulo en polares es equivalente a fijar una recta que pase por el origen (con ese ángulo). Por lo tanto fijar ángulo y calcular límite no es más que un límite direccional (como decís, restringirse a una recta y=mx).
Si bien hay una traducción de la definición de límite en el origen a polares (Ejercicio 4a) esto no es lo mismo que fijar cada ángulo y hacer límite (por la misma razón que la existencia de limites direccionales no prueba la existencia del límite). Es decir, si querés calcular un límite en coordenadas polares vas a tener que verificar que se cumpla esa definición (traducción).
Acá hay algo fino que es que estamos tendiendo a r=0, y los puntos de radio 0 y ángulo cualquiera corresponden todos al mismo punto, el (0,0), es por esto que al pasar a polares y fijarse lo que pasa en el origen hay que tener cuidado porque las coordenadas "pierden inyectividad" ahí.
Fijar un ángulo en polares es equivalente a fijar una recta que pase por el origen (con ese ángulo). Por lo tanto fijar ángulo y calcular límite no es más que un límite direccional (como decís, restringirse a una recta y=mx).
Si bien hay una traducción de la definición de límite en el origen a polares (Ejercicio 4a) esto no es lo mismo que fijar cada ángulo y hacer límite (por la misma razón que la existencia de limites direccionales no prueba la existencia del límite). Es decir, si querés calcular un límite en coordenadas polares vas a tener que verificar que se cumpla esa definición (traducción).
Acá hay algo fino que es que estamos tendiendo a r=0, y los puntos de radio 0 y ángulo cualquiera corresponden todos al mismo punto, el (0,0), es por esto que al pasar a polares y fijarse lo que pasa en el origen hay que tener cuidado porque las coordenadas "pierden inyectividad" ahí.
Favio, si entendí bien entonces, no es suficiente con el límite calculado en coordenadas polares para asegurar que ese es el límite de f(x,y), no? Como dice en el ejercicio 4d) del repartido, el recíproco no se cumple, es decir, no necesariamente se cumple que si el limite de la función en polares es L, el de la función lo es. Esto esta bien? No me queda claro.
Claro, eso mismo, no vale el recíproco. Está bien lo que decís.
Si cambiamos a polares y haciendo tender r a 0 y nos da que existe el límite, no necesariamente tiene que existir el límite de f (de contraejemplo tenemos el ejercicio 4c iii) ). Capaz lo que hay que preguntarse es ¿qué límite estamos tomando? Cuando cambiamos a polares y estudiamos qué pasa en el origen fijate que solo hacemos tender r a 0. ¿Y el ángulo? Por eso digo que lo fino es que el cambio de coordenadas no es un cambio de coordenadas en el punto (0,0).
Por ejemplo, si en lugar de estudiar lo que pasa en el punto (0,0) queremos ver lo que pasa en el punto (1,0) = (cos(0),sen(0)), entonces es equivalente estudiar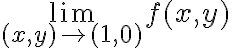
que estudiar 
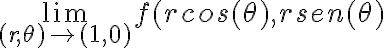porque la función cambio de coordenadas 
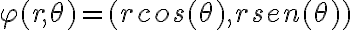definida en 
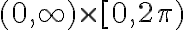sí es una biyección cuando 
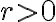y el ángulo varía 
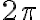. O dicho de otra forma, al punto (1,0) le corresponde solo el par radio-ángulo 
, 
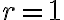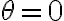. Acá sí podemos hacer cambio de coordenada y límite tranquilos, pero en el (0,0) es distinto, pues todos los puntos 
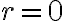y 
cualquiera corresponden al origen.
Si cambiamos a polares y haciendo tender r a 0 y nos da que existe el límite, no necesariamente tiene que existir el límite de f (de contraejemplo tenemos el ejercicio 4c iii) ). Capaz lo que hay que preguntarse es ¿qué límite estamos tomando? Cuando cambiamos a polares y estudiamos qué pasa en el origen fijate que solo hacemos tender r a 0. ¿Y el ángulo? Por eso digo que lo fino es que el cambio de coordenadas no es un cambio de coordenadas en el punto (0,0).
Por ejemplo, si en lugar de estudiar lo que pasa en el punto (0,0) queremos ver lo que pasa en el punto (1,0) = (cos(0),sen(0)), entonces es equivalente estudiar
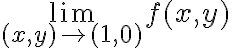que estudiar 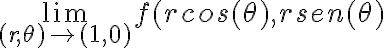porque la función cambio de coordenadas 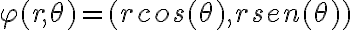definida en 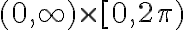sí es una biyección cuando 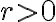y el ángulo varía 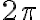. O dicho de otra forma, al punto (1,0) le corresponde solo el par radio-ángulo 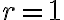, 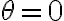. Acá sí podemos hacer cambio de coordenada y límite tranquilos, pero en el (0,0) es distinto, pues todos los puntos 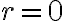y cualquiera corresponden al origen.