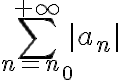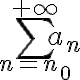Buenas, con mis compañeros estamos teniendo problemas con este ejercicio, particularmente con la serie de la izquierda...
Nosotros en primera instancia pensamos que como tengo (-1) a la n multiplicando a otra función, el límite de el término general no existe y por ende la serie no converge. Luego, viendo la solución, resulta que la serie sí converge, pero en el procedimiento no toman en cuenta ese (-1) a la n, sino que solo se fijan en que la función a la que ese término está multiplicando sí converge (con lo cual estamos de acuerdo). No entendemos porqué ese (-1) a la n "no importa". Les agradezco si pueden ayudarnos.