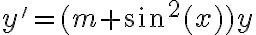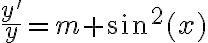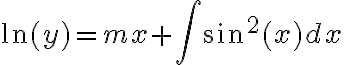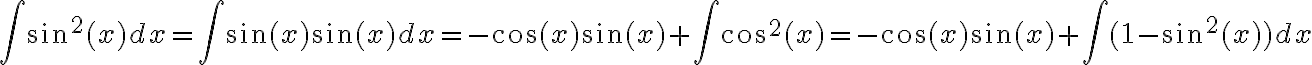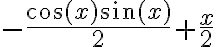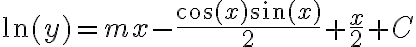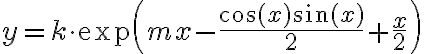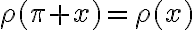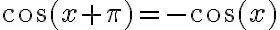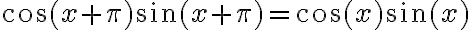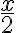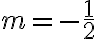
Quería consultar como hacer este ejercicio. Yo lo tome como una ecuación de variables separables e integré y llegue a que:
y(x)= e^ ((2m^2+ 2x-sen2x)/4). k
No se cómo proseguir y usar el dato de que p(x)= p(pi+x), si me pudieran ayudar desde aca a conseguir m les agradecería!