Ecuación Diferencial.

Ecuación Diferencial.

de María Victoria García Alvarez -
Número de respuestas: 2

Buenas.

Estoy haciendo algunas ecuaciones diferenciales del Apóstol y estoy teniendo problemas al reconocer qué tipo de 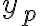y_{p} me serviría. La ecuación es:

y''-2y'+y=x+2xe^x .

La solución en el libro es:

y=(c_{1}+c_{2}x+\frac{1}{3}x^{3})e^{x}+\frac{1}{4}e^{2x}

Saludos y gracias.
En respuesta a María Victoria García Alvarez

Re: Ecuación Diferencial.

de Franco Mateo Vienni Baptista -
Buenas María,

Acá tenés unas notas con el método de selección que es una manera "mecánica" para encontrar soluciones particulares.

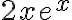Podes separar y encontrar 2 soluciones particulares, una que por resultado te de x y la otra 2xe^x y luego sumarlas para obtener la solución particular buscada.

y''-2y'+y=x a esta ecuación podemos probar con funciones lineales del estilo y(x)=ax+b
Entonces tenemos:
y(x)=ax+b
y'(x)=a
y''(x)=0
Sustituyendo
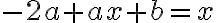-2a+ax+b=x como son polinomios se da la igualdad termino a termino.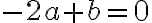

-2a+b=0
a=1 \Rightarrow b=2

Entonces nuestra primera parte de la solución es: x+2

y''-2y'+y=2xe^x a esta ecuación podemos probar con funciones lineales multiplicadas por la exponencial del estilo y(x)=(ax+b)e^x

Si haces las cuentas vas a ver que se anula, entonces tenemos que multiplicar nuestro "intento" de solución por x.

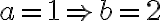
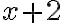
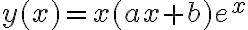Entonces intentamos con soluciones del tipo y(x)=x(ax+b)e^x. Haciendo las cuentas al final nos queda solo una constante por 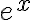e^x así que tampoco nos sirve.

Así que por ultimo multiplicamos nuevamente por x,
y(x)=x^2(ax+b)e^x
y'(x)=x(ax^2+(b+3a)x+2b)e^x
y''(x)=(ax^3+(b+6a)x^2+(4b+6a)x+2b)e^x

Sustituimos:

(ax^3+(b+6a)x^2+(4b+6a)x+2b)e^x-2x(ax^2+(b+3a)x+2b)e^x+x^2(ax+b)e^x=2xe^x

(ax^3+(b+6a)x^2+(4b+6a)x+2b)-2x(ax^2+(b+3a)x+2b)+x^2(ax+b)=2x

(ax^3+(b+6a)x^2+(4b+6a)x+2b)-(2ax^3+(b+3a)2x^2+4bx)+(ax^3+bx^2)=2x

((b+6a)x^2+(4b+6a)x+2b)-((b+3a)2x^2+4bx)+(bx^2)=2x

(b+6a-2b-6a+b)x^2+(4b+6a-4b)x+2b=2x

(4b+6a-4b)x+2b=2x

(6a)x+2b=2x

De donde obtenemos a=\dfrac{1}{3} y b=0

Entonces nuestra segunda parte de la solución particular es: \dfrac{x^3}{3}e^x

Sumando ambas soluciones tenemos y_P(x)=x+2+\dfrac{x^3}{3}e^x

Sabiendo los "criterios" del método de selección nos podíamos haber ahorrado hacer la prueba con x y x^2.

Saludos,
Franco.