Foro Práctico 5

Hola Mariana. Efectivamente, que una integral diverja o que oscile son cosas diferentes (la diferencia es lo que decís: si ese límite da infinito o no existe). En este caso, el límite 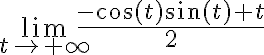$\displaystyle \lim_{t\to +\infty} \frac{-\cos(t)\sin(t)+t}{2}$ da infinito. Intuitivamente lo que pasa es que el $t$ te tira las cosas a infinto y el producto 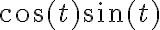$\cos(t)\sin(t)$ no te cambia ese comportamiento, porque en el peor de los casos eso vale 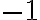$-1$. Formalmente, una forma de verlo es usar que 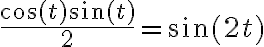$\displaystyle \frac{\cos(t)\sin(t)}{2} = \sin(2t)$, entonces 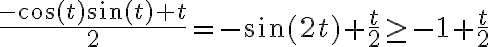$\displaystyle \frac{-\cos(t)\sin(t)+t}{2} = -\sin(2t) + \frac{t}{2} \geq -1 + \frac{t}{2}$ y ese último término se va a $+\infty$.

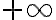Saludos