Foro Práctico 5

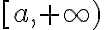Hola Agustina, formalmente lo correcto es separar la integral en dos integrales de primera especie que son las que definimos y sabemos tratar (las de primera especie son las de integrales definidas en $(-\infty,a]$ o $[a,+\infty)$). En este caso podemos dividir la integral en dos: 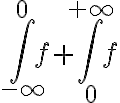$\int_{-\infty}^0 f + \int_{0}^{+\infty} f$. Oservando que la función 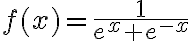$f(x)=\frac{1}{e^x+e^{-x}}$ es par (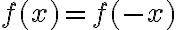$f(x)=f(-x)$), estas dos integrales valen lo mismo.
Digo todo esto porque hay que tener cuidado cuando hacemos ambos límites al mismo tiempo, pensá por ejemplo qué pasaría con $\int_{-\infty}^{+\infty}xdx$.

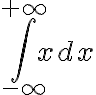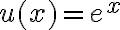En este caso particular, como ambas integrales convergen, no hay problema con lo que hiciste. El cambio de variable $u(x)=e^x$ funciona bien porque 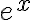$e^x$ es una biyección entre 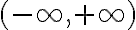$(-\infty,+\infty)$ y $(0,+\infty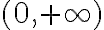)$ que es derivable con inversa derivable.
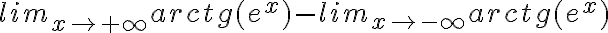Ojo con algunas formalidades al calcular el límite: debería decir $lim_{x\to +\infty} arctg(e^{x}) - lim_{x\to -\infty} arctg(e^{x})$ (en lo que escribiste no aparece la $x$ sino que "evaluas" en los infinitos)

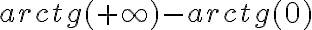Lo que no entiendo es por qué te da distinto si "deshacés" el cambio de variable antes, en ambos quedaría $arctg(+\infty) - arctg(0)$, no?