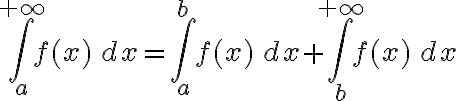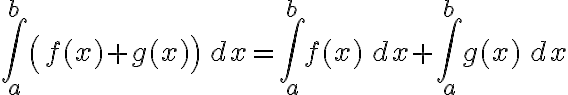Convergencia de integrales impropias mixtas.

Convergencia de integrales impropias mixtas.

de Franco Mateo Vienni Baptista -
Número de respuestas: 2

Buenas a todos,

En el video numero 16 de OpenFING (aproximadamente minuto 36:30) , el profesor argumenta que al separar la integral impropia mixta en sus sumandos problemáticos nos basta que uno diverja para decir que la integral original era divergente.

¿Esto no puede llevar a problemas? Ejemplifico:
En el Práctico 5 - Ejercicio 6 (i) se concluye que la impropia es convergente, pero que pasa si hacemos lo siguiente:

\displaystyle\int_{0}^{+\infty}\dfrac{\cos(x)}{\sqrt x}dx = \int_{0}^{1}\dfrac{\cos(x)}{\sqrt x}dx + \int_{1}^{+\infty}\dfrac{\cos(x)}{\sqrt x}dx

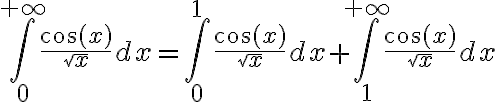
Si nos concentramos solamente en la convergencia del segundo sumando por ejemplo: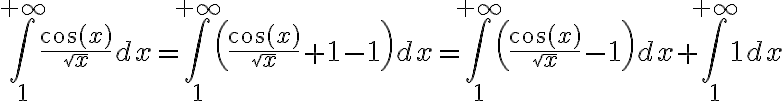
\displaystyle\int_{1}^{+\infty}\dfrac{\cos(x)}{\sqrt x}dx = \int_{1}^{+\infty}\left(\dfrac{\cos(x)}{\sqrt x} + 1 - 1\right)dx=\int_{1}^{+\infty}\left(\dfrac{\cos(x)}{\sqrt x} - 1\right)dx+\int_{1}^{+\infty}1dx

Y ahora tenemos un sumando que diverge, siguiendo nuestra definición de convergencia para integrales impropias mixtas la integral en cuestión diverge.

De manera similar podríamos "argumentar" que cualquier impropia mixta que queramos diverge. Esto es obviamente falso, ¿pero el error esta en la definición?

¿Interprete erróneamente lo que intento expresar el profesor? ¿Qué definición podemos usar para solventar este problema?

Saludos,
Franco.
En respuesta a Franco Mateo Vienni Baptista

Re: Convergencia de integrales impropias mixtas.

de Bernardo Marenco -

Hola. Fijate que la diferencia entre el primer y el segundo ejemplo es que en el primer caso separás la integral como:

\displaystyle \int_a^{+\infty} f(x) \, dx = \int_a^b f(x) \, dx + \int_b^{+\infty}f(x) \, dx

Es decir, obtenés dos sumandos usando la aditividad respecto al dominio de integración, pero lo que estás integrando en cada sumando es lo mismo. Eso es lo que hacemos para las impropias mixtas, y decimos que convergen si y solo si ambos sumandos convergen.

En el segundo ejemplo lo que estás haciendo es usar la linealidad respecto al integrando, manteniendo el intervalo de integración. Algo así:

\displaystyle \int_a^{b} \left( f(x)+g(x)\right) \, dx=\int_a^{b} f(x) \, dx+\int_a^{b} g(x) \, dx

En ese caso, como bien decís, la integral original puede ser convergente aunque cada sumando no lo sea. No hay incongruencia entre estas dos cosas, porque son dos cosas diferentes: en un caso se trata de la linealidad respecto al dominio de integración (manteniendo la misma función adentro de la integral) y en el otro estás hablando de la linealidad respecto al integrando (manteniendo el dominio de integración).

Saludia