Práctico 1 - Ejercicio 2 (Ejercicios Complementarios)

Práctico 1 - Ejercicio 2 (Ejercicios Complementarios)

de Ivana Castillo Rivas -
Número de respuestas: 4

Hola, estaba intentando este ejercicio pero no sabría como aplicarlo a una función (sí a un número complejo, como el w que se indica en la letra). Como podría encarar el ejercicio? Gracias!

En respuesta a Ivana Castillo Rivas

Re: Práctico 1 - Ejercicio 2 (Ejercicios Complementarios)

de Favio Piran -
Hola Ivana

Nos podemos definir una función 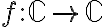f: \mathbb{C} \to \mathbb{C} dada por 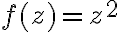f(z)=z^2, pues como dice la letra, por cada 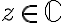z\in \mathbb{C} existe un único complejo 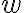w tal que 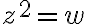z^2=w. El problema planteado es intentar definir una función "inversa" para f, es decir una función raíz cuadrada. Para empezar ya vemos que no puede existir una inversa global: podés corroborar que f no es inyectiva (en 1 y en -1 vale igual, por ejemplo). Más aún, vimos que dado z distinto de 0 existen dos raíces complejas para z, así que ya vemos el primer problema: la elección de la raíz de z. El siguiente paso, un poco más fino, es definir explícitamente alguna de estas elecciones y ver si hay algún problema. Para esto es recomendabble pensar en coordenadas polares.

Y más relacionado a tu pregunta de función, tené en cuenta que justamente queremos definir una función "raíz" y esto implica que hay que especifiar el dominio de esta.

Si te trancás avisá.
Saludos!
En respuesta a Favio Piran

Re: Práctico 1 - Ejercicio 2 (Ejercicios Complementarios)

de Diego Subeldia Loureiro -
Hola Favio, aprovecho a continuar el planteo. Si yo defino f:R+U(0)-->R+U(0), no tendría los mencionados problemas para definir raíz de z, verdad?
El conjunto de salida y el de llegada (reales positivos unión 0) deberían estar elevados al cuadrado, ¿no?
Mi confusión viene por el lado de que en el ejercicio nos dice que discutamos posibles definiciones de una función "raíz cuadrada", pero no especifica que debamos analizar si es posible definir una inversa de f:C→C dada por f(z)=z2. Por eso digo que si defino la función como puse más arriba no tendría esos inconvenientes.

Saludos y gracias.
En respuesta a Diego Subeldia Loureiro

Re: Práctico 1 - Ejercicio 2 (Ejercicios Complementarios)

de Bernardo Marenco -

Hola Diego. El problema de definir una función "raíz cuadrada" es exactamente el problema de "definir una inversa de 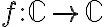f:\mathbb{C}\to \mathbb{C} dada por 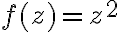f(z)=z^2" (justamente, la raíz cuadrada se define como la inversa de la función "elevar al cuadrado"). Para los complejos, ya vimos que no es posible definir una inversa de 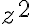z^2 en todo 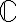\mathbb{C} por lo que decía Favio arriba. Una posible solución es la que vos decís: restringir el dominio a los reales no negativos y definir la inversa ahí. El tema es que esa solución me deja gusto a poco: tal vez sea posible definir la inversa en un conjunto que no solo involucre a los reales (y por lo tanto, sea posible definir el concepto de raíz cuadrada para al menos algunos complejos no reales). Para hacer eso, está bien la sugerencia de Favio de arriba de escribir el complejo z en polares.

Saludos