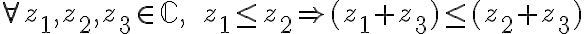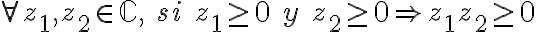Foro Práctico 1

Hola. Este ejercicio pide probar que no es posible definir una relación de orden para los complejos, es decir, no es posible ponerle una noción de "quién es menor que quién" a 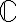$\mathbb{C}$. La idea es mostrar que no se puede definir un conjunto de complejos "positivos" que cumplan los axiomas de orden que viste en Cálculo en una Variable (que algunos son los que Florencia ponía más arriba).

Supongamos que puedo definir una noción de "complejos positivos", es decir, puedo definir una relación de orden, que voy a escribir con el símbolo 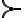$\succ$ en vez de 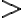$>$ para que quede claro que es una relación que puede ser distinta a la de los reales. Así, 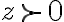$z \succ 0$ quiere decir que $z$ es positivo con esa relación de orden. 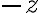Uno de los axiomas de orden que viste en CDIV es que solo uno de $z$ o $-z$ puede ser positivo. Siguiendo la sugerencia de Florencia, supongamos que 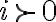$i \succ 0$ (es decir, que 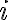$i$ es "positivo"). Entonces 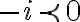$-i \prec 0$ (es decir, 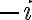$-i$ tiene que ser "negativo"). Pero el axioma de orden del producto nos dice que si 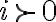$i \succ 0$, entonces 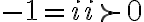$-1 = i i \succ 0$. Ok, eso es un poco raro porque estaríamos diciendo que el 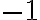$-1$ es positivo, que suena raro pero no es una contradicción porque mi relación de orden no tiene por qué ser la misma que la de 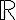$\mathbb{R}$. 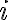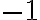Sigamos multiplicando: si tanto $i$ como $-1$ con positivos (de nuevo, según la relación de orden 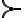$\succ$), entonces su producto 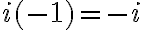$i(-1) = -i$ tiene que ser positivo, es decir, 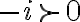$-i \succ 0$. Pero ya vimos que si 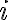$i$ es positivo, 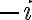$-i$ tiene que ser negativo, así que tenemos una contradicción. Si suponés que 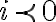$i \prec 0$ también llegás a una contradicción similar.

Saludos