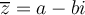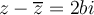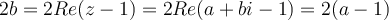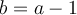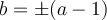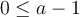Buenas. No logro resolver este ejercicio... intenté hallar condiciones para la parte real y la parte imaginaria de z, pero no llegué a nada. Si me pueden tirar un pique o algo, les agradezco mucho.
Por ejemplo el b
Sea
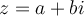 entonces
entonces 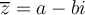 por tanto
por tanto 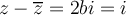 por tanto
por tanto 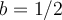 de ahí que la representación grafica te quedara la recta
de ahí que la representación grafica te quedara la recta 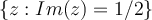 ya que la parte real no afecta si se cumple o no la ecuación, espero que te haya sido de ayuda
ya que la parte real no afecta si se cumple o no la ecuación, espero que te haya sido de ayudaCualquier cosa pregunta
Como es la norma de alguien tambien cumple que 0≤a−1"
Hola. Que "la ecuación es invariante por conjugar" quiere decir que si  es solución de la ecuación, entonces su conjugado
es solución de la ecuación, entonces su conjugado 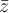 también es solución. Podés verificarlo cambiando
también es solución. Podés verificarlo cambiando  por
por 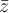 en la ecuación de la parte e y viendo que si
en la ecuación de la parte e y viendo que si  la verifica entonces necesariamente
la verifica entonces necesariamente 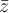 también. Eso quiere decir que si hallás un conjunto de complejos que resuelven la ecuación, entonces el conjunto de los conjugados de esos complejos también tiene que ser solución.
también. Eso quiere decir que si hallás un conjunto de complejos que resuelven la ecuación, entonces el conjunto de los conjugados de esos complejos también tiene que ser solución.
La parte de "Como es la norma de alguien también cumple que  " se refiere a que el lado izquierdo de la ecuación es la norma de "alguien" (siendo ese alguien
" se refiere a que el lado izquierdo de la ecuación es la norma de "alguien" (siendo ese alguien  ). Si escribís
). Si escribís 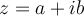 entonces
entonces  , y
, y  . Como eso tiene que ser igual a
. Como eso tiene que ser igual a  , la igualdad queda
, la igualdad queda  . Como lo de la izquierda es mayor o igual que 0, para que esa igualdad tenga sentido se tiene que cumplir que
. Como lo de la izquierda es mayor o igual que 0, para que esa igualdad tenga sentido se tiene que cumplir que 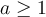 .
.
Saludos