No se como encarar este ejercicio, tampoco se como aplicar el dato :![]()
para cada k = {1, ... , 8}
No se como encarar este ejercicio, tampoco se como aplicar el dato :![]()
para cada k = {1, ... , 8}
![\sqrt[8]{2^8} \sqrt[8]{2^8}](https://eva.fing.edu.uy/filter/tex/pix.php/ae7c430c710748b10e0b70fc60d60fa1.gif) y que sus argumentos son los de las raíces octavas de la unidad, de esa manera sabes que cada
y que sus argumentos son los de las raíces octavas de la unidad, de esa manera sabes que cada 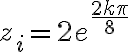 (usas la formula de las raíces n-esimas) , una vez que tienes todas las raíces es fácil ver si las afirmaciones son verdaderas o falas, espero te sirva
(usas la formula de las raíces n-esimas) , una vez que tienes todas las raíces es fácil ver si las afirmaciones son verdaderas o falas, espero te sirva