Hola, Rodrigo. Por la manera en que la solución define el ángulo 
, la masa pasa por el punto D cuando se cumple 
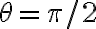. Esta es la posición cuando el plano del disco queda vertical, y el punto diametralmente opuesto a la masa queda en su posición más alta (punto C).
En la parte anterior se obtiene una relación para las variables del sistema de la forma
El razonamiento es que esa expresión solo puede ser cierta para los valores de tales que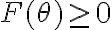 
, porque la cantidad a la izquierda, 
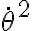no puede ser negativa (es un número al cuadrado). Entonces, luego, se analiza bajo qué condiciones efectivamente se cumple
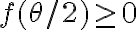
¿Se entiende?
Técnicamente, se plantea una condición necesaria para que el sistema pueda llegar a ese valor, pero no se sabe si es suficiente... estaría interesante encontrar un argumento que justifique que ese valor es alcanzado (hay que fijarse en las ecuaciones de movimiento y las condiciones iniciales)
Suerte!
NC
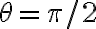, la masa pasa por el punto D cuando se cumple . Esta es la posición cuando el plano del disco queda vertical, y el punto diametralmente opuesto a la masa queda en su posición más alta (punto C).En la parte anterior se obtiene una relación para las variables del sistema de la forma
El razonamiento es que esa expresión solo puede ser cierta para los valores de
tales que 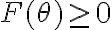, porque la cantidad a la izquierda, 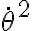no puede ser negativa (es un número al cuadrado). Entonces, luego, se analiza bajo qué condiciones efectivamente se cumple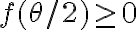¿Se entiende?
Técnicamente, se plantea una condición necesaria para que el sistema pueda llegar a ese valor, pero no se sabe si es suficiente... estaría interesante encontrar un argumento que justifique que ese valor es alcanzado (hay que fijarse en las ecuaciones de movimiento y las condiciones iniciales)
Suerte!
NC