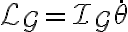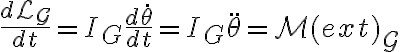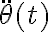Hola, Lucas. A ver si podemos aclarar estos puntos....
El momento angular respecto al centro de masa G queda (según z)
y la segunda cardinal respecto a G queda (siempre según z)
O sea, en la segunda cardinal aparece la aceleración angular dada por 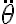 , que a su vez es la derivada de la velocidad angular
, que a su vez es la derivada de la velocidad angular  .
.
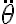 , que a su vez es la derivada de la velocidad angular
, que a su vez es la derivada de la velocidad angular  .
.(en la solución se usa esta integral implícitamente, dejando los detalles a cargo del lector).
Espero haber ayudado a aclarar.
Suerte,
NC
NC