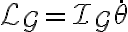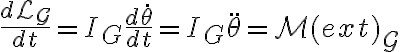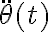Buenas. No entiendo en este ejercicio de dónde saca la expresión de la derivada segunda de tita por R^2 por la masa sobre 2 y lo iguala al torque externo en el disco 2, no sería la derivada primera de tita (velocidad angular)? porque imagino que está igualando la derivada del momento angular (L) con los momentos externos no?
En respuesta a Lucas Facundo Casales Carballo
Re: Segundo parcial 2017 ejercicio 2.a.ii
de Nicolás Casaballe -
Hola, Lucas. A ver si podemos aclarar estos puntos....
El momento angular respecto al centro de masa G queda (según z)
y la segunda cardinal respecto a G queda (siempre según z)
O sea, en la segunda cardinal aparece la aceleración angular dada por 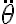 , que a su vez es la derivada de la velocidad angular
, que a su vez es la derivada de la velocidad angular  .
.
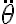 , que a su vez es la derivada de la velocidad angular
, que a su vez es la derivada de la velocidad angular  .
.(en la solución se usa esta integral implícitamente, dejando los detalles a cargo del lector).
Espero haber ayudado a aclarar.
Suerte,
NC
NC