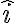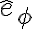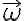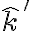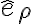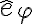MecNew: Descomposición de w en ej 1

Buenas, pude llegar al resultado correcto, pero para ello tuve que hacer una suposición que no se como justificarla.

Lo que hice fue descomponer w, que estaba según el eje i, en dos versores que acompañaran a la barra, como se muestra en la figura. Cuando descompuse w ahí, utilice que solo se encontraba en dos versores, (k' y e_ro), creo que esto está bien para el instante inicial, pero no me queda claro si estaría bien para todo tiempo, pues e_ro rota, y e_phi también, entonces en un cierto t*, el lugar que ocupaba e_ro al principio, será ocupado por e_phi, haciendo que para ese instante t*, la descomposición de w sea otra. Mi duda es, cómo hago la descomposición de w para todo tiempo, o esto no es necesario? Si no fuera necesario, por qué no lo es?

Gracias, saludos!

Re: Descomposición de w en ej 1

de Enzo Spera - lunes, 21 de junio de 2021, 13:06

Estimado, la descomposición que realisaste es correcta. Si bien es cierto que tus versores verdes rotan, la velocidad anguar siempre es según

$\hat{i}$ y el ángulo

$\alpha$ es constante por lo que, aunque roten, tu descomposición se mantiene valída en todo momento.
Para visualizar eso, por ejemplo, dibuja la situación después de que el dispositivo rote media vuelta y repetí la descomposición. Vas a ver que sin importar en que posición esté, la descomposición queda siempre igual y que el vector

$\hat{e}_\phi$ , aunque rota, siempre está perpendicular a

$\hat{i}$ .

Saludos

Re: Descomposición de w en ej 1

de Nicolás Casaballe - lunes, 21 de junio de 2021, 13:20

Hola, Iván. Me gustó tu dibujo.

La manipulación de los vectores que hiciste es correcta. Eso se debe a que, por la geometría del sistema, los tres vectores $\vec \omega$ , $\hat k'$ y $\hat e_\rho$ permanecen en un mismo plano a medida que el tiempo transcurre. En cambio, $\hat e_\varphi$ siempre aparece en dirección perpendicular a la velocidad angular, de manera que esta tiene componente nula en esa dirección, para todo tiempo.

Puede ser de ayuda, para visualizar, una representación 3D que se puede acceder desde la página del curso: https://eva.fing.edu.uy/mod/page/view.php?id=110541

Estrictamente hablando, quedaría pendiente justificar por qué el vector de velocidad angular $\vec \omega$ se mantiene siempre en la línea AB. La razón de fondo es que la transformación de un sistema fijo (absoluto) a un sistema solidario al disco (relativo) es una rotación sencilla alrededor del eje AB, lo cual determina el vector de la velocidad angular. La justificación formal es algo engorrosa, donde hay que combinar lo que hemos visto en los temas de cinemática del principio del curso y algunos de los resultados referidos a cuerpos rígidos (p. ej. ejercicio 5.9).

Saludos,