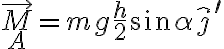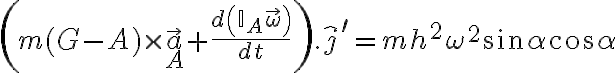Hola, se me ocurrio igualar el Momento en A al torque en A para obtener α en funcion de w. No se como hallar el torque en A y no se si mi Momento en A es correcto.
Hola,
No se si entiendo bien tus notas, pero creo que no tenes bien la geometria del problema. La barra se encuentra en un plano perpendicular al eje OA. Me da la impresion que vos tenes la barra en el plano dado por OA y el eje vertical, aunque capaz que no estoy entendiendo bien tus notas.
La idea del ejercicio es aplicar la segunda cardinal con respecto al punto A, que es un punto del rigido. Hay que tener cuidado que el punto A tiene aceleracion no nula.
Es importante tambien calcular los torques sobre el rigido con respecto al punto A. Con respecto a A, hay torque debido a la articulacion y al peso. La clave es que como la articulacion es cilindrica, el torque de la articulacion con respecto a A es cero en la direccion del eje de giro de la articulacion cilindrica (la direccion OA en este caso). Al proyectar la 2da cardinal en esta direccion desaparece el torque de la articulacion, solo aparece el torque del peso
espero que esto te sirva
cualquier cosa volve a preguntar y si entendi mal tu planteo por favor aclaramelo
saludos
g
Tenias razon, lo habia entendido mal el ejercicio. Es posible que puedan subir la resolucion de este?
El momento del peso te debería quedar algo así:
(siendo j' el versor móvil a lo largo del eje de la articulación cilíndrica)
Luego,
Igualando estas dos cantidades llegás a los valores posibles de 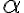 .
.
Dejo la parte de la letra, que a mi parecer decía que la barra estaba en un plano que formaba un ángulo alfa con la vertical.
"el ángulo alfa que forma la barra con el plano vertical es constante". Para que esto sea verdad, creo que hay dos opciones, o bien la barra gira en un plano como el que digo, o bien la barra está como tu dices, por qué descarto mi idea?
Gracias, saludos!
 con la vertical por el efecto de las pseudofuerzas del problema. Si la velocidad angular
con la vertical por el efecto de las pseudofuerzas del problema. Si la velocidad angular  cambia, por ejemplo, el ángulo
cambia, por ejemplo, el ángulo  cambiaría.
cambiaría. Espero aclare tus dudas.
Saludos