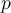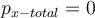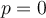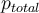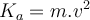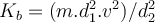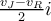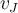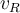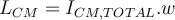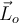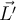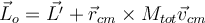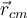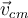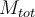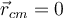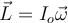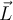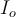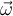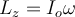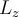Hola! Gracias por las respuestas! Voy a ir comentando con respecto a cada punto lo que entendí y lo que no me quedó muy claro:
1) Esto no lo entendí jaja, calcule la energia cinética en la parte (a) es decir cuando los patinadores, luego del choque, quedan girando con una distancia entre ellos igual al largo de la barra (d1 = 2,29m) y me dio
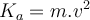
, y luego calcule la energía cinética de la parte (b) que es cuando los patinadores, luego del choque, quedan girando con una distancia entre ellos menor que el largo de la barra (quedan a una distancia d2 = 0,940m), porque ellos tiran de la barra para acercarse, y me dio
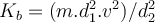
. Pude ver que el momento angular del sistema (desde el CM del mismo) en la parte (a) es mayor que en la parte (b) (por que los patinadores están más lejos), y la velocidad angular con la que rotan luego del choque en la parte (a) (w = 0,945rad/s) es menorque la de la parte (b) (w' = 9,12rad/s).
O sea, es como que al estar más cerca disminuye el momento angular pero aumenta la velocidad angular. Sin embargo, la energía cinética en ambas situaciones (cuando luego de chocar estan a 2,29m y cuando estan a 0,940m) es distinta, la de la parte (b) es mayor que la de la parte (a) y no logro ver por qué. Pense que tal vez tendría que ver con que la fuerza esa que hacen al tirar de la barra para acercarse hace algun tipo de trabajo, pero no tengo idea de como es esta fuerza, si es conservativa o no, etc. y además es una fuerza interna al sistema, entonces me confunde un poco.
2) Ahí va, ahí entendí, me había entreverado, esto es algo que pasa particularmente en la parte (a) y (b) porque en ambos casos P antes del choque es 0 y no hay fuerzas externas en ningún momento, entonces P del sistema en todo momento es 0. (Porque la fuerza que hacen al tirar de la barra es interna no?). Mientras que en las partes (d) y (e), si bien aquí también se conserva P, el P antes del choque no es 0 (por lo tanto en ningun momento lo es). ¿ Entonces cuando se habla de la "cantidad de momento total del sistema" es simplemente la cantidad de movimiento lineal del sistema? ¿No tiene nada que ver el momento angular del mismo?
3) En el parte (d) lo que pasa es que ahora los patinadores antes del choque tienen la misma masa pero vienen con velocidades distintas, luego de que choquen los patinadores van a rotar alrededor del cento de masa del sistema pero además este centro de masa se va a desplazar, particularmente luego del choque la velocidad del centro de masa será
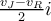
. Mi tema es que al momento de calcular los momentos angulares lo hago respecto a este centro de masa, y el resultado de estos momentos depende de las velocidades con que venian los patinadores, luego igualo estos momentos y así despejo la velocidad angular con la que rotarán luego del choque, esta velocidad angular por lo tanto, dependerá de las velocidades lineales con las que venían los patinadores. Entonces, yo calculé los L respecto del CM, entonces al calcularlos, ¿debería utilizar las velocidades respecto al CM, o respecto a un punto fijo? Porque las velocidades
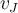
y
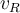
son respecto a un referencial inercial, y yo estoy calculando L respecto al CM que se está moviendo. ¿No debería hacer movimiento relativo ahí? ¿La velocidad angular desde que referencial está entonces, el CM o un punto fijo?
4) Gracias jaja. Tenía entendido del teórico que la fórmula
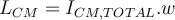
no se puede utilizar para cualquier cuerpo o para cualquier sistema, que esto no vale de manera genérica (incluso mostramos algún ejemplo de un sistema donde esto no se cumplía), como que vimos que esto vale únicamente para cuerpos que tengan simetría de revolución respecto al eje de giro. ¿No es así?
Y respecto a si este sistema tiene simetría, no sé, yo no lo veo simétrico jajja, tipo es una barra que tiene una masa chica de un lado y una grande del otro, entonces no termino de ver bien si tiene simetría de revolución o no. Supongo que si porque lo supuse, use la fórmula y llegue al resultado jsja, pero si hago otro ejercicio ¿qué puedo hacer?, ¿simplemente supongo que todo será simétrico y hago todo así nomás o cómo puedo darme cuenta si puedo usar la fórmula o no?
Perdón por atomizar a preguntas otra vez. Gracias!
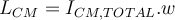 . Mi consulta es, tenía entendido que esta forma de calcular el momento angular era únicamente para cuerpos rígidos simétricos que rotan alrededor del eje de simetría, pero este cuerpo no es simétrico, porque una de las masas es más grande que la otra, entonces no entiendo por qué se puede utilizar.
. Mi consulta es, tenía entendido que esta forma de calcular el momento angular era únicamente para cuerpos rígidos simétricos que rotan alrededor del eje de simetría, pero este cuerpo no es simétrico, porque una de las masas es más grande que la otra, entonces no entiendo por qué se puede utilizar.