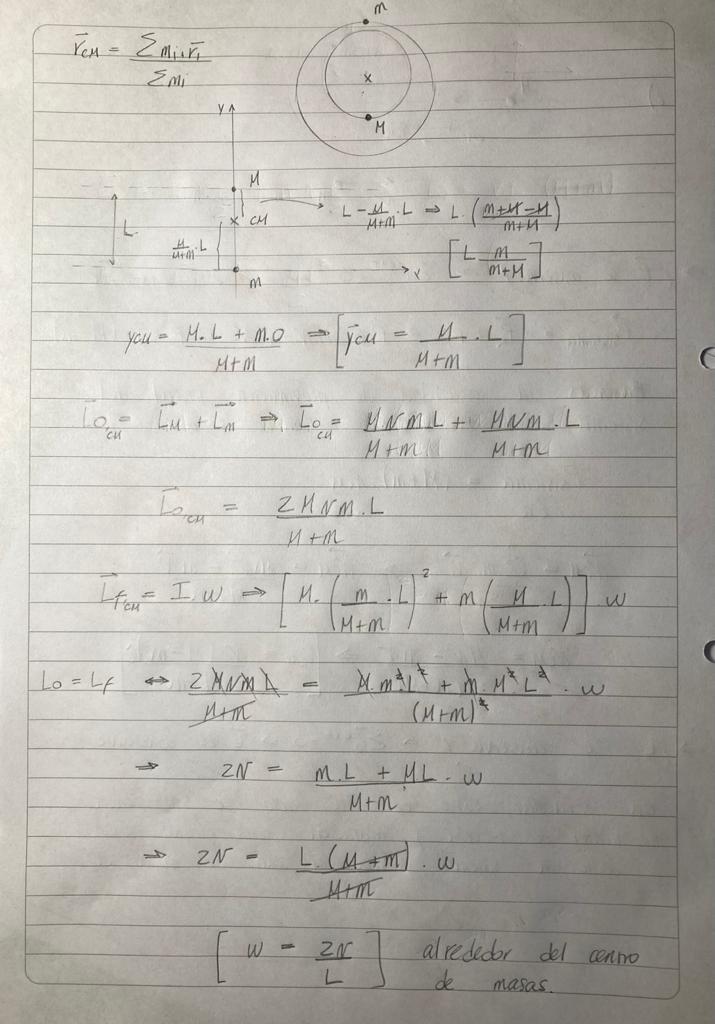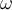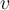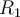Ejercicio 6 - e

Ejercicio 6 - e

de Nicolas Brignoni Dardano -
Número de respuestas: 8

Se me ocurrió encarar este ejercicio de la manera que se ve en la foto adjunta, esto es calculando la posición del centro de masa y luego calcular el momento angular desde un sistema solidario al centro de masa. En este caso el centro de masa esta mas próximo a la partícula con mayor masa. 

Lo intente hacer de esta manera y llegue al resultado pero no se si la forma es del todo correcta.

Saludos y Gracias

Nicolás

Adjunto fisica.jpeg
En respuesta a Nicolas Brignoni Dardano

Re: Ejercicio 6 - e

de Juan Manuel Ferres Rodriguez -
A mí se me ocurrió para la parte d) que para un instante cualquiera la cantidad de movimiento del sistema no es nula porque las velocidades son diferentes entonces el sistema además de rotar se traslada, está bien eso?
Lo mismo en la parte e) pero en este caso porque las masas son diferentes.


En respuesta a Juan Manuel Ferres Rodriguez

Re: Ejercicio 6 - e

de Carla Yelpo -
Hola, Nicolás y Juan Manuel

El planteo de Nicolás es correcto y permite determinar la velocidad angular con la que rota el sistema alrededor del centro de masas. Pero como bien agrega Juan Manuel, en las partes (e) y (d) el centro de masas ya no estará en reposo. Entonces, debemos determinar también esa velocidad, para terminar de describir el movimiento del sistema.

¿Se dan cuenta cómo calcularlo?

¡Saludos!
En respuesta a Carla Yelpo

Re: Ejercicio 6 - e

de Nicolas Brignoni Dardano -
Gracias Carla y Juan. Yo había calculado la velocidad del centro de masa en la carrilla anterior usando conservación de momento lineal pero me interesaba preguntar bien que pasa si me tomo un sistema de referencia solidario al centro de masa para calcular el momento angular. Esta duda surgió porque no nos dio el tiempo para verlo en el practico al que asisto y viendo resoluciones en grupos y comparando me di cuenta de que como el resultado es el mismo que en la parte (a), esto es, cuando las masas y las velocidades son idénticas, entonces lo calculaban como si el centro de masa equidistara de ambas partículas y esto no es así por lo que entiendo.

Entonces me faltaría agrear la velocidad del centro de masa al análisis cuantitativo y pronto?

Gracias de nuevo,

Saludos
En respuesta a Carla Yelpo

Re: Ejercicio 6 - e

de Victoria Analia Olivera Romero -

Buenas, a mi no me está dando el ω en la parte e, comparto lo que hice a ver si me ayudan a ver el error. Gracias.

Adjunto 1688747402516 (1).jpg
En respuesta a Victoria Analia Olivera Romero

Re: Ejercicio 6 - e

de Alejandro Silva -
Buenas Victoria,

Un detalle importante de este ejercicio es que la relación entre como se mueve el centro de masas y la velocidad angular no tiene porque ser  v_{cm}= R \omega .  sin ir más lejos, en los primeros ejemplos que ambos patinadores giraban entorno a un punto fijo, los patinadores tienen cierta velocidad angular  \omega , pero su centro de masas está quieto.

Ahora, si tenemos los dos patinadores girando con cierta velocidad ( \omega \), que es lo que tenemos que hallar, y además su centro de masas se traslada a cierta velocidad   v_{cm}, ¿Cómo nos quedan las velocidades tangenciales?

Pues queda como el dibujo de abajo




Como sabemos que las masas tienen velocidad v, tenemos que 

  v = v_{cm} + R_1 \omega

donde  R_1 es la distancia de la masa de más arriba al centro de masas.
De esa ecuación se despeja omega.

Espero haberte ayudado,

Saludos,
A. Silva