Hola, en este ejercicio yo me tome las coordenadas en el versor i,j y k de la distancia a la ciudad. Lo que no entiendo es si la velocidad que es hacia el este, me la tendría que tomar solo en i. Porque en ese caso no tendría momento angular en j y k el avión no? Gracias
Buenas Ayelén,
Efectivamente, si te tomas coherentemente los versores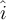 y
y 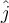 para que coincidan con el Este y Norte respectivamente, entonces la velocidad solo tiene componente en
para que coincidan con el Este y Norte respectivamente, entonces la velocidad solo tiene componente en 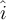 . Sin embargo esto tiene como consecuencia justo lo contrario a lo que decís, porque el momento angular solo tendría componentes es la dirección
. Sin embargo esto tiene como consecuencia justo lo contrario a lo que decís, porque el momento angular solo tendría componentes es la dirección 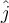 y
y 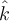 , no teniendo componente en la dirección
, no teniendo componente en la dirección 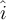 . Esto proviene del hecho que el momento angular lo definimos a partir de un producto vectorial. De forma general nos quedaría:
. Esto proviene del hecho que el momento angular lo definimos a partir de un producto vectorial. De forma general nos quedaría:

De ese producto vectorial el término no aporta porque esos vectores son colineales (el ángulo que se forma entre ellos es 0) pero los otros dos si aportan, dando resultados en las componentes
no aporta porque esos vectores son colineales (el ángulo que se forma entre ellos es 0) pero los otros dos si aportan, dando resultados en las componentes 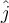 y
y 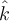 .
.
Espero que con esto puedas llegar al resultado, pero sino volve a consultar.
Saludos,
Juan Llaguno
Efectivamente, si te tomas coherentemente los versores
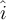 y
y 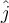 para que coincidan con el Este y Norte respectivamente, entonces la velocidad solo tiene componente en
para que coincidan con el Este y Norte respectivamente, entonces la velocidad solo tiene componente en 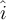 . Sin embargo esto tiene como consecuencia justo lo contrario a lo que decís, porque el momento angular solo tendría componentes es la dirección
. Sin embargo esto tiene como consecuencia justo lo contrario a lo que decís, porque el momento angular solo tendría componentes es la dirección 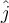 y
y 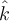 , no teniendo componente en la dirección
, no teniendo componente en la dirección 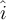 . Esto proviene del hecho que el momento angular lo definimos a partir de un producto vectorial. De forma general nos quedaría:
. Esto proviene del hecho que el momento angular lo definimos a partir de un producto vectorial. De forma general nos quedaría:
De ese producto vectorial el término
 no aporta porque esos vectores son colineales (el ángulo que se forma entre ellos es 0) pero los otros dos si aportan, dando resultados en las componentes
no aporta porque esos vectores son colineales (el ángulo que se forma entre ellos es 0) pero los otros dos si aportan, dando resultados en las componentes 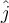 y
y 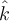 .
.Espero que con esto puedas llegar al resultado, pero sino volve a consultar.
Saludos,
Juan Llaguno
Hola, estoy intentando con este ejercicio pero el valor que está en la solución para la dirección y (norte) me da en z (arriba), y no me doy cuenta como hacer el cálculo para la dirección y (entiendo que necesito el ángulo entre la distancia y la velocidad pero no se cómo sacarlo).
Buenos días,
En primer lugar recordemos la definición de momento angular, la cual depende de algún punto de referencia, en este caso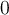 .
.
En primer lugar recordemos la definición de momento angular, la cual depende de algún punto de referencia, en este caso
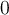 .
.Seguramente como recuerdas, si queremos hallar el módulo del momento angular este nos queda de la forma
Sin embargo, no es la única forma de hallar el momento angular. Otra forma es hacer el producto vectorial escribiendo los vectores 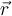 y
y 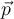
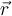 y
y 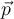
en una base de versores, vamos a hacer esto.
En este caso si consideramos los versores en este ejercicio como  en las direcciones este, norte y arriba respectivamente, podemos escribir los vectores
en las direcciones este, norte y arriba respectivamente, podemos escribir los vectores 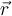 y
y 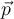 .
.
 en las direcciones este, norte y arriba respectivamente, podemos escribir los vectores
en las direcciones este, norte y arriba respectivamente, podemos escribir los vectores 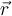 y
y 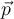 .
.Como dice la letra:

Los vectores nos quedan de la forma
Como los versores son ortogonales entre sí, tenemos que  ,
,  y
y  . De manera que solo sobreviven los productos cruzados.
. De manera que solo sobreviven los productos cruzados.
 ,
,  y
y  . De manera que solo sobreviven los productos cruzados.
. De manera que solo sobreviven los productos cruzados._____________________________________________________________________________________________________
Te invito a hacer la cuenta
Alejandro, no entiendo de dónde sale esa √2 en los versores, creo que eso es lo que me está faltando.
Buenas, si tengo un vector de largo r, en la dirección noreste por ejemplo.
Si descompongo el vector:
Si descompongo el vector:
Como el ángulo es 45°, tanto el seno como el coseno de 45° es raíz de dos.
Saludos,
A. Silva
Gracias, ahora si me dio. Saludos.