Hola.
Disculpas que se me pasó este mensaje y recién ahora lo estoy contestando.
La H que mencionás de la página 18 es la tasa de entropía.
Es cierto que el teorema de Shannon habla de variables aleatorias, no de procesos, pero con un poco de trabajo adicional se llega a que el teorema de Shannon implica que la tasa de entropía es una cota inferior para el largo de código esperado normalizado (práctico 3, ejercicio 5.1). LZ77 se puede aplicar a cualquier cadena de texto; en particular para cada n LZ77 define un código de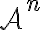
en 
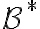(fixed to variable).
La forma de extender el resultado a procesos (no iid) es como en el ejercicio 5 del práctico 3. Reemplazar H(X) por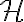
en el resultado que comentás para iid no tiene por qué funcionar directamente. Sí es cierta la primera desigualdad (cota inferior), que es lo que dice el ejercicio 5.1. Para la segunda (cota superior para un código óptimo) lo que podés afirmar es algo como lo que dice el ejercicio 5.2. También es cierto que se cumple que 
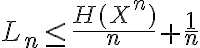, pero 
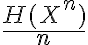podría estar lejos de 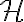si n no es suficientemente grande.
Capaz que tenés dudas sobre el ejercicio 5. En ese caso lo podemos ver en la clase, o por acá si te resulta más cómodo.
Saludos,
Álvaro
Disculpas que se me pasó este mensaje y recién ahora lo estoy contestando.
La H que mencionás de la página 18 es la tasa de entropía.
Es cierto que el teorema de Shannon habla de variables aleatorias, no de procesos, pero con un poco de trabajo adicional se llega a que el teorema de Shannon implica que la tasa de entropía es una cota inferior para el largo de código esperado normalizado (práctico 3, ejercicio 5.1). LZ77 se puede aplicar a cualquier cadena de texto; en particular para cada n LZ77 define un código de
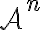en 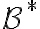(fixed to variable).La forma de extender el resultado a procesos (no iid) es como en el ejercicio 5 del práctico 3. Reemplazar H(X) por
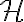en el resultado que comentás para iid no tiene por qué funcionar directamente. Sí es cierta la primera desigualdad (cota inferior), que es lo que dice el ejercicio 5.1. Para la segunda (cota superior para un código óptimo) lo que podés afirmar es algo como lo que dice el ejercicio 5.2. También es cierto que se cumple que 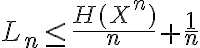, pero 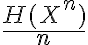podría estar lejos de 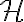si n no es suficientemente grande.Capaz que tenés dudas sobre el ejercicio 5. En ese caso lo podemos ver en la clase, o por acá si te resulta más cómodo.
Saludos,
Álvaro