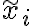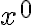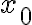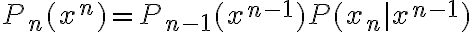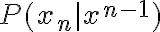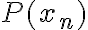Foro de consultas

Buenas, me surgieron las siguientes dudas respecto a esta codificacion (las 2 primeras estoy suponiendo que de alguna forma tengo un algoritmo o implementacion real del codigo, por mas que no se use el la practica):

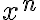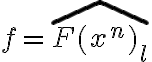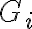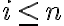1) No me queda claro como el decodificador, con solo la palabra de codigo (particularmente: sin tener el largo de la secuencia a decodificar), decodificar correctamente la secuencia. Si tengo una secuencia $x^{n}$ y su codigo $f = \hat{F(x^{n})_{l}$ (El "F techo" truncado en l bits, no pude arreglar el latex), entonces puedo calcular $G_{i}$ para $i \leq n$. Luego, nada me asegura que 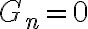$G_{n} = 0$, por lo que yo podria intentar calcular 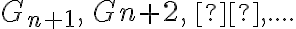$G_{n+1} ,\, G{n+2} ,\,  , ....$. Entonces cual seria la condicion de parada del algoritmo de decodificacion

2) Si fuera a implementar el algoritmo de decodificacion para SFE, necesitaria "tener toda la secuencia de entrada en memoria" , porque para empezar a decodificar necesito 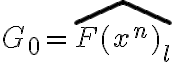$G_{0} = \hat{F(x^{n})_{l}$, para lo que necesito leer toda la secuencia y despues recien puede empezar con la decodificacion. Es correcto esto?

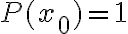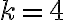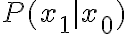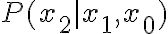3) En las diapositivas (y en clase) esta que por convencion tenemos $P(x_{0}) = 1$. No me termina de quedar claro porque es asi. Ademas, si yo tuviera por ejemplo un modelo markoviano de orden $k = 4$ (y en particular donde el estado inicial no esta fijo, sino que tiene una distribucion de probabilidad), entonces no me es suficiente conocer $P(x_{1} | x_{0})$ o $P(x_{2} | x_{1}, x_{0})$ . Entonces, como calcularia 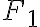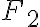$F_{1}$ , $F_{2}$ y $F_{3}$ ?

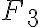Saludos,

Rafael.