Buenas, repasando el teorico (de LZ77) me surgieron un par de dudas sobre codigos optimos y la optimalidad de LZ77 (pido disculpas por poner alguna parte de las ecuaciones en palabras, pero la notacion exede mi conocimiento de LaTeX)
En la pagina 18 de de las diapos de LZ77 se dice:(lo marcado como Theorem)
"el limite cuando el tamaño de la ventana tiende a infinito del limite cuando n tiende a infinito del ratio promedio de compresion de LZ77 es igual a H"
Primeramente, con esa H se refiere a la entropia de la variable aleatoria del proceso o a la tasa de entropia del proceso?
Despues se dice que dicho teorema implica optimalidad debido a la cota inferior de Shannon. Nosotros lo que entendi que teniamos enunciado es que dada una variable aleatoria X cualquiera y l(X) el largo un codigo optimo para X, entonces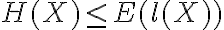 
y 
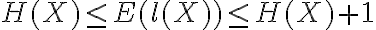
Entonces la cota de Shannon aplica para variables aleatorias, no para procesos estocasticos.
Ademas lo habiamos definido en un contexto donde los codigos era todos del tipo fixed to varible length y LZ77 es un codigo variable to variable length, entonces aplica para todo tipo de codigo el teorema de Shannon?
Despues extendimos el teorema a bloques, pudiendonos hacercarnos arbitrariamente a la entropia de la variable aleatoria que genera dichos bloques. Esto lo hicimos para secuencias iid y dijimos que valia tambien para secuencias no iid. Repasando, me di cuenta que no me quedo del todo claro la justificacion.
Para procesos no iid en vez de enunciar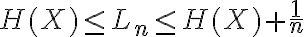 
, podriamos expresarlo con la tasa de entropia? Es decir: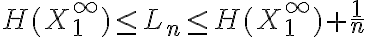
En concreto: No termino de ver como el teorema de Shannon que enunciamos y el teorema del limite del ratio de compresion promedio dan la optimalidad de LZ77, por los motivos que aclare mas arriba(que tambien son dudas que me quedaron).
Desde ya muchas gracias,
Saludos,
Rafael.
Hola.
Disculpas que se me pasó este mensaje y recién ahora lo estoy contestando.
La H que mencionás de la página 18 es la tasa de entropía.
Es cierto que el teorema de Shannon habla de variables aleatorias, no de procesos, pero con un poco de trabajo adicional se llega a que el teorema de Shannon implica que la tasa de entropía es una cota inferior para el largo de código esperado normalizado (práctico 3, ejercicio 5.1). LZ77 se puede aplicar a cualquier cadena de texto; en particular para cada n LZ77 define un código de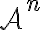
en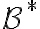 
(fixed to variable).
La forma de extender el resultado a procesos (no iid) es como en el ejercicio 5 del práctico 3. Reemplazar H(X) por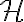
en el resultado que comentás para iid no tiene por qué funcionar directamente. Sí es cierta la primera desigualdad (cota inferior), que es lo que dice el ejercicio 5.1. Para la segunda (cota superior para un código óptimo) lo que podés afirmar es algo como lo que dice el ejercicio 5.2. También es cierto que se cumple que 
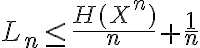, pero 
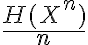podría estar lejos de 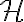si n no es suficientemente grande.
Capaz que tenés dudas sobre el ejercicio 5. En ese caso lo podemos ver en la clase, o por acá si te resulta más cómodo.
Saludos,
Álvaro
Disculpas que se me pasó este mensaje y recién ahora lo estoy contestando.
La H que mencionás de la página 18 es la tasa de entropía.
Es cierto que el teorema de Shannon habla de variables aleatorias, no de procesos, pero con un poco de trabajo adicional se llega a que el teorema de Shannon implica que la tasa de entropía es una cota inferior para el largo de código esperado normalizado (práctico 3, ejercicio 5.1). LZ77 se puede aplicar a cualquier cadena de texto; en particular para cada n LZ77 define un código de
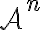en 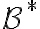(fixed to variable).La forma de extender el resultado a procesos (no iid) es como en el ejercicio 5 del práctico 3. Reemplazar H(X) por
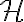en el resultado que comentás para iid no tiene por qué funcionar directamente. Sí es cierta la primera desigualdad (cota inferior), que es lo que dice el ejercicio 5.1. Para la segunda (cota superior para un código óptimo) lo que podés afirmar es algo como lo que dice el ejercicio 5.2. También es cierto que se cumple que 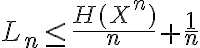, pero 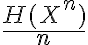podría estar lejos de 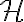si n no es suficientemente grande.Capaz que tenés dudas sobre el ejercicio 5. En ese caso lo podemos ver en la clase, o por acá si te resulta más cómodo.
Saludos,
Álvaro