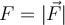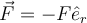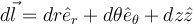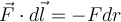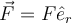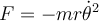Primer Parcial 2006 Ejercicio 2

Primer Parcial 2006 Ejercicio 2

de Carlos Nicolas Imperial Luzardo -
Número de respuestas: 2

Buenas, mi duda radica sobre la parte C de este ejercicio, dado que la fuerza F del hilo aporta al movimiento de la partícula, es coherente que el trabajo de dicha fuerza para ir desde a hasta b (b<a) sea positivo, pero al plantear la definición de trabajo, el producto escalar F.dr  es igual a 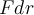F dr ya que creo yo que ambos vectores apuntan hacia el centro O, llegando así a un trabajo de dicha fuerza negativo, en la solución de esta parte escriben que F.dr  es igual a  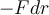- F dr , que estaría mal en mi razonamiento?
En respuesta a Carlos Nicolas Imperial Luzardo

Re: Primer Parcial 2006 Ejercicio 2

de Nicolás Casaballe -
Hola, Carlos. Lo que estás pensando sobre los signos y el trabajo es correcto.

Lo que confunde es la notación que se usa, que en la solución no está del todo aclarada. Allí se utiliza la variable F para indicar el módulo de la fuerza:
    F= |\vec F | .
El vector de esa fuerza (en coordenadas cilíndricas, p.ej.) queda escrito como
    \vec F = - F \hat e_r
porque, efectivamente, apunta hacia el centro y el vector unitario es saliente.

Cuando planteamos la integral para el trabajo, consideramos un vector de desplazamiento infinitesimal que podemos representar como
    d \vec l = dr \hat e_r + d \theta \hat e_\theta + dz \hat z
Entonces resulta
    \vec F \cdot d \vec l = - F dr
------
Para mi gusto, esta notación no es la mejor. Yo prefiero que las variable que uso representen las componentes de los vectores y no sus módulos. En ese caso, yo escribiría la fuerza como
    \vec F = F \hat e_r
donde ahora la variable F me queda negativa:
    F = - mr {\dot \theta} ^2

Es lo mismo, pero distinto, pero igual lo mismo.

Same Same But Different GIFs - Get the best GIF on GIPHY
-----
¿se entiende?
Suerte,
NC